Аннотация научной статьи по строительству и архитектуре, автор научной работы — Матвеев А. Д.
Предложены вероятностный и энергетический методы нахождения коэффициентов запаса прочности, которые приближенно учитывают характер распределения напряжений в конструкциях. Показан комплексный анализ прочности конструкций на основе применения некоторых положений вероятностного и энергетического методов.
Похожие темы научных работ по строительству и архитектуре , автор научной работы — Матвеев А. Д.
Анализ прочности упругих конструкций со случайными параметрами с применением эквивалентных условий прочности
Определение коэффициента запаса прочности, вероятности разрушения и срока службы для совокупности упругих деталей, состоящих из различных материалов
Прогнозирование усталостной прочности стержня с выточкой из наноструктурного титанового сплава при симметричном циклическом изгибе
Текст научной работы на тему «Определение коэффициентов запаса прочности конструкций с учетом распределения напряжений»
Контурные и фактические площади контактов, их удельные давления и коэффициенты трения при температурах выше 6000С
Запас прочности и допускаемые напряжения
№ Показатель Сталь 20 Сталь 65Г
ці = 0,08 ці = 0,26 ці = 0,08 ці = 0,26
1 Асі, мм2 820,0 504,7 801 493,2
2 Рсі,МПа(кгс/мм2) 11,4(1,14) 7,1(0,71) 11,6(1,16) 7,1(0,71)
3 Асі2, мм2 724,5 343,7 712,8 335,8
4 Рсі2,МПа(кгс/мм2) 10,3(1,03) 5,2(0,52) 10,5(1,05) 5,3(0,53)
5 Аті, мм2 10,8 4,16 7,06 2,73
6 Рті,МПа(кгс/мм2) 865,0(86,5) 865,0(86,5) 1316,0(131,6) 1316,0(131,6)
7 Аті2, мм2 8,7 2,0 5,7 1,35
8 Рті2,МПа(кгс/мм2) 865,0(86,5) 865,0(86,5) 1316,0(131,6) 1316,0(131,6)
9 dp1, мм 0,02 0,018 0,018 0,016
10 dp12, мм 0,02 0,017 0,018 0,015
11 М2(1) 0,646 0,640 0,570 0,560
12 М2(12) 0,641 0,630 0,570 0,560
Выполненные расчеты позволяют перейти к следующему этапу работы по определению скоростей нагрева дисков в диапазоне температур выше 6000С, мощностей тепловых потоков, условий и причин их радиальной усадки и деформации.
1. Справочник по расчету и конструированию контактных частей сильноточных электрических аппаратов / под ред. В.В. Афанасьева. — Л.: Энергоатомиздат, 1988.
2. Детали машин: сб. материалов по расчету и конструированию. — Изд. 2. Кн. 1, 2 / под ред. Н.С. Ачеркана. — М.: Машиностроение, 1953.
3. Демкин, Н.Б. Контактирование шероховатых поверхностей / Н.Б. Демкин. — М.: Наука, 1970.
4. Попова, Л.Е. Диаграмма превращения аустенита в сталях и бета-растворах в сплавах титана / Л.Е. Попова, А.А. Попов // Справочник термиста. — 3-е изд. — М.: Металлургия, 1991.
5. Крагельский, И.В. Трение и износ / И.В. Крагельский. — М.: Машиностроение, 1968.
6. Термическая обработка в машиностроении / под ред. Ю.М. Лахтина. — М.: Металлургия, 1980.
УДК 539.3 АД. Матвеев
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ЗАПАСА ПРОЧНОСТИ КОНСТРУКЦИЙ С УЧЕТОМ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ
Предложены вероятностный и энергетический методы нахождения коэффициентов запаса прочности, которые приближенно учитывают характер распределения напряжений в конструкциях. Показан комплексный анализ прочности конструкций на основе применения некоторых положений вероятностного и энергетического методов.
3.2.8 Коэффициент запаса прочности стропов
Введение. В настоящее время широко применяются конструкции, которые состоят из пластичных материалов. Как известно [1-3], коэффициент п запаса прочности конструкции, состоящей из пластичного материала и имеющей статическое нагружение, определяют по формуле
где ат — предел текучести материала; ат — максимальное эквивалентное напряжение, действующее в конструкции [1-3].
Отметим, что коэффициент п, определяемый по формуле (а), неточно оценивает прочностные свойства конструкции. Это связано с тем, что коэффициент n не отражает характер распределения напряжений в конструкциях.
Рассмотрим пример. Пусть две конструкции, состоящие из одинакового пластичного материала, имеют различный характер распределения напряжений. При этом первая конструкция является равнонапряженной. В этом случае эквивалентные напряжения af конструкции постоянны во всей ее области, т.е. аЭ =а1 = const. Вторая конструкция имеет один концентратор напряжений (большие напряжения возникают в окрестности только одной точки области конструкции). Пусть а2 = max(a2), где аЭ — функция
эквивалентных напряжений второй конструкции. При а1 = а2 = ат в силу (а) получаем п1 = = 1,
п2 = = 1, т.е. коэффициенты запаса прочности п1, п2 соответственно первой и второй конструкций
равны. Как известно [3], конструкция (состоящая из пластичного материала) разрушается, если в ней возникает область Sp пластического состояния определенных размеров, S с S , S — область конструкции. В
области Sp эквивалентные напряжения постоянны и равны ат. При а1 = ат первая конструкция разрушается, так как вся ее область находится в пластическом состоянии (Sp = S). У второй конструкции при а2 = ат пластическое состояние возникает только в одной точке ее области (в этой точке max(a2) = а2). Поэтому вторая конструкция не разрушается и продолжает выполнять свои функции.
Итак, при равенстве максимальных эквивалентных напряжений (при аэт =а1 =а2 =ат) вторая конструкция (имеющая один концентратор напряжений) является более прочной, чем первая (равнонапряженная) конструкция. Таким образом, характер распределения напряжений в конструкциях влияет на их прочностные свойства.
Следует отметить, что причинами разрушения конструкций при их эксплуатации также могут быть силовые воздействия технологического характера и производственные дефекты. Такими причинами, например, являются: монтажные усилия (которые могут возникнуть при монтаже конструкций), микротрещины, царапины, остаточные напряжения (которые могут возникнуть при изготовлении конструкций), дефекты сварных соединений, нарушение условий эксплуатации конструкций и т.д. [3].
В силу этих причин разрушение конструкции может произойти в любой точке ее области (например, в окрестности микротрещины, возникшей в процессе изготовления конструкции). Поскольку возникновение такого рода причин носит вероятностный характер [3], то возможное разрушение конструкции в каждой точке ее области можно рассматривать как событие, которое может совершаться с некоторой вероятностью. В связи с этим при анализе прочности и надежности конструкций используют параметр, показывающий вероятность разрушения конструкции [2]. В настоящий момент вероятности разрушения конструкций определяют без учета распределения напряжений.
В данной работе предложены вероятностный и энергетический методы определения коэффициентов запаса прочности конструкций [4]. Эти методы приближенно учитывают характер распределения напряжений в конструкциях. В основе вероятностного метода лежит соотношение, которое представляет коэффициент запаса прочности конструкции через вероятность ее разрушения.
При этом вероятность разрушения конструкции определяется с учетом распределения напряжений. Энергетический метод реализуется в конечноэлементной форме [5]. В данном методе используется функция, выражающая уровень энергии опасного состояния конструкции через удельные потенциальные энергии формоизменения всех конечных элементов дискретной модели.
Эта функция строится с учетом распределения напряжений в конструкции. Показан комплексный метод анализа прочности конструкций, в котором используются некоторые положения энергетического и вероятностного методов. Приведен пример расчета.
1. Вероятностный метод. Как известно [2], вероятность p разрушения конструкции возрастает при уменьшении ее коэффициента n запаса прочности и наоборот: увеличение коэффициента запаса прочности конструкции приводит к уменьшению вероятности ее разрушения. В связи с этим вводим следующее
предположение, которое лежит в основе вероятностного метода. Считаем, что между величинами n, p , которые отвечают различным нагружениям конструкции, существует взаимно однозначная связь вида n = f (p), где функция f отражает ряд факторов, влияющих на прочность конструкции. Положения вероятностного метода состоят в следующем.
Положение 1.1. Конструкция состоит из пластичного материала, имеет статическое нагружение и определенные условия крепления. Считаем, что коэффициенты запаса прочности и вероятности разрушения данной конструкции, отвечающие различным ее нагружениям, связаны функциональной зависимостью вида
где n — коэффициента запаса прочности и p — вероятность разрушения конструкции,
f (p) — непрерывная функция, имеющая обратную f -1, т. е. p = f ~l(n),
Функция f (p) для данной конструкции отражает ее физические свойства, форму и размеры, харак-
тер нагружения, качество изготовления, условия крепления и эксплуатации.
Положение 1.2. Конструкцию представляем областями Vt (V = U Vi, где V — область конструкции,
N — число областей Vt), в которых расположены концентраторы напряжений.
Положение 1.3. Считаем, что разрушение конструкции может произойти в любой из ее областей: V1 . VN, причем возможные разрушения конструкции в областях V1 . VN являются независимыми (по вероятности) событиями.
Следует отметить, что дефекты, которые могут вызвать разрушение конструкции, возникают в областях V1 . VN независимо друг от друга (например, возникновение микротрещин при изготовлении конструкции).
Положение 1.4. Коэффициент запаса прочности ni области Vt конструкции определяем по формуле
где 7т — предел текучести; (г1э — максимальное эквивалентное напряжение области Vt, т.е.
о1э = max (7э); 7э — функции эквивалентных напряжений конструкции.
Положение 1.5. Считаем, что коэффициент запаса прочности ni и вероятность разрушения pt области Vi связаны соотношением
ni = f (pi), i = 1. N. (4)
В первом приближении функцию f (p) с учетом (2) представим в виде
f (p) = а0(1 — p), а0 = const, а0 > 0. (5)
В этом случае в силу (1), (5) имеем
Отметим, что для функции f (p) вида (5) существует обратная, т.е. эта функция удовлетворяет положению 1.1. При использовании представления (6) параметры nt, pi области Vi, согласно положению 1.5, удовлетворяют равенству
n; =«0(1 — pi), i = 1. N. (7)
При анализе прочности конструкций, которые состоят из пластичных материалов и имеют статическое нагружение, широко используют четвертую теорию прочности [1]. Коэффициент n0 запаса прочности конструкции по четвертой теории прочности вычисляют по формуле
где ат — максимальное эквивалентное напряжение конструкции, определенное по четвертой теории прочности [1].
Рассмотрим приближенный способ определения коэффициента а0. Согласно четвертой теории, прочность конструкции эквивалентна прочности стержня (образца), который работает на растяжение и состоит из такого же материала, что и конструкция. При этом напряжение в стержне равно аэт и коэффициент
запаса прочности стержня-образца (как и конструкции) равен п0 = 7т / 7эт. Пусть вероятность разрушения стержня (образца) равна р0. Тогда существует такое а0 > 0, что п0 = а0 (1 — р0).
Значение р0 можно определить с помощью испытаний, проведенных для стержней (образцов), коэффициенты запаса прочности которых равны п0 и которые состоят из такого же материала, имеют такое же качество изготовления и такие же условия эксплуатации, как и данная конструкция. Заметим, что в приближенных расчетах параметр р0 может быть задан [2]. Пусть для коэффициента п0 параметр р0 известен. Тогда из равенства
п0 =а0(1 — р0) получаем
Испытания показывают, что вероятность р0 разрушения стержня (образца) зависит от качества его
т и 7т. В силу (8), (9) и коэффициент а0
изготовления и условий эксплуатации, от значений напряжений 7эт и 7т. В силу (8), (9) и коэффициент а
также зависит от значений 7т, 7т, от качества изготовления и условий эксплуатации стержня (образца), т.е. конструкции. С помощью (7), (9) вероятность р1 разрушения области у представим как
р1 = 1 — (1 — р0), I = 1. N. (10)
Пусть р1 > 0. Из р1 > 0 в силу (3), (8), (10) следует неравенство
7Э >7т (1 — р0) . (11)
Так как значение вероятности не может быть отрицательным, то рассматриваем такие области у
конструкции, напряжения 71э в которых удовлетворяют условию (11). Пусть рг > 0 для I = 1. N . Считая возможные разрушения конструкции в областях у. VN независимыми (по вероятности) событиями (см. положение 1.3), находим вероятность рг разрушения конструкции хотя бы в одной из ее областей У . VN по формуле [6].
рг = 1 — П (1 — р1 )• (12)
Согласно (6), параметру рг отвечает коэффициент пг, т.е. имеем пг =а0(1 — рг). С учетом (9) коэффициент запаса прочности пг конструкции (отвечающий вероятностному методу) равен
В силу (3), (10), (12) имеем зависимость рг = рг(71. 7^), т.е. значение рг зависит от макси-
мальных эквивалентных напряжений 7^. 7Э^ соответственно областей у. УN. Следовательно, значение рг вероятности разрушения конструкции приближенно отражает ее характер распределения напряжений. Величина а0 (как отмечалось ранее) зависит от значений напряжений 7эт, 7т, от качества изготовления и условий эксплуатации конструкции. Согласно (13), пг = пг (а0, рг). Таким образом, коэффи-
циент nr приближенно отражает характер распределения напряжений в конструкции, ее физические свойства (т.е. предел текучести 7т), качество изготовления и условия эксплуатации.
Рассмотрим пример. Пусть конструкция имеет q (q > 1) подобластей Vj . Vq (т.е. пусть конструкция имеет q концентраторов напряжений), в которых максимальные эквивалентные напряжения 7;j. 73q
отличаются от максимального эквивалентного напряжения 7m конструкции на достаточно малую величину, 73m = max (7j7^). Поэтому принимаем: 71э =73m (i = 1. q) и в силу (3), (8), (10) имеем: nt = n0 =7т / 73m, pt = p0, i = 1. q. Пусть для коэффициента n0 известно p0. Тогда вероятность разрушения pr (q) и коэффициент запаса прочности nr (q) данной конструкции в силу (12), (13) (pi = p 0, i = 1,—, q) соответственно равны:
pr(q) = 1 — (1 — po)q, nr(q) = no(1 — po)q-1. (14)
(при 73m = const) не меняется (n0 =7т / 73m = const). Итак, в данном примере коэффициент nr более точно оценивает прочность конструкции, чем коэффициент n0.
2. Энергетический метод. Рассмотрим конструкцию, которая состоит из пластичного материала и имеет статическое нагружение. Пусть для данной конструкции построено конечноэлементное решение. В центре тяжести КЭ Ve (e = 1. N, N — общее количество КЭ) определяем эквивалентное напряжение
7^ по четвертой теории прочности [1]. Считаем, что в области КЭ Ve: 7; = const, e = 1. N . В этом
случае удельную потенциальную энергию формоизменения Пф КЭ Ve представим в форме [1]
где E — модуль Юнга, ц — коэффициент Пуассона, e = 1. N .
при e = m, если 73m =7т. Как известно, всякое изменение формы КЭ Ve (т.е. изменение энергии формоизменения КЭ Ve) приводит к изменению формы КЭ Vm (т.е. к изменению энергии формоизменения КЭ
Vm), e = 1. N, e Ф m. Причем, чем дальше КЭ Ve находится от КЭ Vm, тем меньше КЭ Ve влияет на
изменение формы КЭ Vm, т.е. тем меньше КЭ Ve ,,изменяет» энергию формоизменения КЭ Vm. Таким образом, энергии формоизменения КЭ Ve, e = 1. N, e Ф m, влияют (в разной степени) на энергию формоизменения КЭ Vm. В связи с этим вводим следующее предположение (которое лежит в основе энергетического метода). Считаем, что уровень энергии Пр опасного состояния конструкции (при 7; = const в области КЭ Ve, e = 1. N ) определяется значениями удельных потенциальных энергий формоизменения
‘кретиой мопепи те считаем что «П_ _ (-П1 АА n
всех КЭ дискретной модели, т.е. считаем, что Пр = Пр (ПфП^). Положения энергетического метода
состоят в следующем.
Положение 2.1. Конструкцию представляем разбиением на КЭ Ve, e = 1. N, N — общее количество КЭ. Разбиение области конструкции на КЭ такое мелкое, что считаем: в области КЭ Ve: 7; = const, где 7Э; — эквивалентное напряжение КЭ Ve, посчитанное по четвертой теории прочности (в центре тяжести КЭ Ve).
Положение 2.2. Считаем, что энергия Пр опасного состояния конструкции определяется обобщенной удельной потенциальной энергии формоизменения Пm КЭ Vm (в котором возникает максимальное эквивалентное напряжение конструкции), т. е. считаем Пр = П 0m.
Положение 2.3. Энергию П0m находим по формуле
где Пm — энергия, которую „порождает” КЭ Ve в КЭ Vm (e = 1. N, e Ф m).
Положение 2.4. Энергия Пm имеет вид
где F(rem) — непрерывная строго убывающая функция (функция влияния); r^ — расстояние между центрами тяжести КЭ Ve и Vm. Функция влияния F удовлетворяет условиям: F(0) = 1, F(<^) = 0. Итак,
согласно положениям 2.2-2.4, имеем Пр = Пр (Пф. nN).
Положение 2.5. Считаем, что прочность конструкции эквивалентна прочности стержня (образца), который работает на растяжение. При этом обобщенная удельная потенциальная энергия формоизменения
Пm КЭ Vm равна удельной потенциальной энергии формоизменения Пс стержня (образца), т.е.
П0 П 7ЭЧ (1 + М) (70э )2 (16)
где 7,Э — напряжение стержня (образца).
Напряжение 7,Э назовем обобщенным эквивалентным напряжением конструкции.
Положение 2.6. Считаем, что конструкция находится в опасном состоянии, если П0m = Пс (7т), т.е.
согласно (16), если 70 = 7т .
Принимаем F (rem) = exp
, где 2ro — диаметр КЭ Vm. Тогда согласно положению 2.4,
Используя положение 2.3 и формулы (15), (17), энергию П0m запишем в форме
3E e=1 Сравнивая (16), (18), получаем
1 + Z^expHf / ro) , (19)
где ае = гэе / гэт; ае < 1, так как гэт >гэе ПРИ е = 1. N, е ф т; гэт = шахГгэм).
Коэффициент запаса прочности пэ конструкции, отвечающий энергетическому методу, определяем по формуле
Согласно (19), (20), имеем nэ = nэ (af ,■■■,а% ) , т.е. значение коэффициента nэ зависит от напря-
прочности пэ приближенно отражает характер распределения напряжений в конструкциях.
Рассмотрим пример. Пусть гэт =7т и гэе = 7т, е = 1. q; q > 1 (т.е. в области Бр, состоящей из КЭ У1. Уq, возникает пластическое состояние). Пусть КЭ У1 находится в центре области Б р. Используя формулу (19), имеем
а0(q) = аТл 1 + У exp(-rm / r0) + Уa2 exp(-rf / r0), (21)
При увеличении числа q (при увеличении размеров области Sp пластического состояния конструкции) в силу (21) возрастает обобщенное эквивалентное напряжение а0 (q) конструкции. Согласно (20), при возрастании а0 (q) уменьшается коэффициент nэ запаса прочности конструкции, т.е. уменьшается время ее эксплуатации (что подтверждается на практике). Отметим, что при аэт = ат коэффициент n0 запаса прочности конструкции (определяемый по известной формуле (8)) равен n0 = ат / аэт = 1 и с увеличением числа q значение коэффициента n0 не изменяется. Итак, в данном примере коэффициент nэ более точно оценивает прочность конструкции, чем коэффициент n0.
3. Комплексный метод. Данный метод анализа прочности конструкций основан на применении формул вероятностного и энергетического методов. Рассмотрим этапы реализации комплексного метода. Пусть конструкция состоит из пластичного материала, имеет статическое нагружение и q концентраторов напряжений. Пусть для конструкции построено конечноэлементное решение.
В центре тяжести КЭ Ve по четвертой теории прочности определяем эквивалентное напряжение аэе, e = 1. N, N — общее количество КЭ. Считаем, что в области КЭ Ve: аэе = const. Пусть в центрах непересекающихся областей V1, . Vq
конструкции расположены концентраторы напряжений, V = U V1, где V — область конструкции. Для об-
ласти Vi находим максимальное эквивалентное напряжение а^. = max (аэе), N. — количество КЭ об! e=1. N.
1 + У ae2 exp(-remi / Го ) , (22)
где ae =аэе / аэт., e = 1. N., гm — расстояние между центрами тяжести КЭ Ve и V, (1 < т. < N.), 2r0 — диаметр КЭ Vm., i = 1. q.
где і = 1. q, р0 — известно.
Пусть рІ > 0, і = 1. q. Тогда вероятность рк разрушения конструкции хотя бы в одной из об-
ент запаса прочности пк конструкции (отвечающий комплексному методу)
4. Результаты численных экспериментов. Рассмотрим анализ прочности двумерного изотропного однородного линейно-упругого тела размерами 72h x 72h (h = G,5), которое испытывает плоское напряженное состояние [7] и расположено в декартовой системе координат xOy (рис.).
Модуль Юнга тела Е = 1, коэффициент Пуассона /л = 0,3. При у = 0 имеем и = V = 0, граница крепления тела на рисунке отмечена штриховкой. Тело в точках с координатами (72к, ), где
= 30к + к (> -1), > = 1. 30, нагружено силами qx = 1,2 (см. рис.). При решении данной задачи по методу конечных элементов [5] используем дискретную модель, состоящую из квадратных КЭ 8е (е = 1. 5184) первого порядка со стороной к. В центре тяжести КЭ 8е посчитаны эквивалентные напряжения аЭ по четвертой теории прочности [1]. В таблице даны значения эквивалентных напряжений, действующих в окрестности крепления тела, где х. = 0,5к + к (г -1), хг+4 = 69,5к + к(г -1), уг = 0,5к + к (г -1), г = 1,2,3; х4 = 20,5к . Расчеты показывают, что в точке А тела с координатами х = 71,5к; у = 0,5к (см. рис.) действует эквивалентное напряжение аэА = 2,404, которое является мак-
y I x xi x 2 x 3 x 4 x5 x 6 x 7
Уо 2,156 1,570 1,332 0,766 1,478 1,751 2,404
У 2 1,948 1,705 1,438 0,779 1,607 1,915 2,196
y 3 1,710 1,630 1,469 0,792 1,652 1,846 1,947
В точке B тела с координатами x = 0,5h; y = Q,5h (см. рис.) действует эквивалентное напряжение j3B = 2,156. Итак, в окрестностях точек A, B, т. е. в областях S0, S2 (см. рис.), тело имеет два концентратора напряжений. При этом напряжение
Область S (S ) размерами 30h x 30h представлена КЭ Se, e = 1. 900. Отметим, что даль-
нейшее увеличение размеров областей S , S при данном выборе функции влияния не приводит к суще-
ственному изменению результатов. Пусть максимальное эквивалентное напряжение области S1 ( S2) возникает в КЭ S0, причем в области S1: а0э =J3A, в области S2: а0э =J3B. Для областей SO, S2 обобщенные эквивалентные напряжения jQ, jQ (считая, что в области КЭ Se: j3e = const) вычисляем по формулам (см. (22))
1 + £ae2exp(-re1I ro) = 2,698,
где ae =J3e I J3A (J03 = J3A), rQ = 0,5h , г] — расстояние между центрами тяжести КЭ Se и S0,
1 + У a;2 exp(-re11 ro) = 2,416,
где ae = а3е I j3b JO = J3B).
Пусть вероятность разрушения данной конструкции для коэффициента п0 равна 0,01, т.е. пусть
р0 = 0,01. Используя формулы (23), для областей £ , £ находим коэффициенты запаса прочности: п* = ат 1а0) = 1,483, п2 = ^т /
Краснояр. гос. ун-т. — Красноярск, 2006. — 18 с. — Деп. в ВИНИТИ. №1298 — В2006.
5. Зенкевич, О. Метод конечных элементов в технике / О. Зенкевич. — М.: Мир, 1975.
6. Корн, Г. Справочник по математике для научных работников и инженеров / Г. Корн, Т. Корн — М., 2003.
7. Самуль, В.И. Основы теории упругости и пластичности / В.И. Самуль. — М.: Высш. шк., 1970.
УДК 631.3(075.8) Н.И. Селиванов, В.С. Кирин, Р.А. Эбель
ОЦЕНКА ТЯГОВО-СЦЕПНЫХ СВОЙСТВ КОЛЕСНОГО ТРАКТОРА К-701
Получены параметрические уравнения связи буксования с коэффициентом использования веса; установлены максимальные и допустимые значения тягового КПД, определяющие ширину рациональных тяговых диапазонов; определены условия рационального агрегатирования тракторов с переменными массоэнергетическими параметрами в составе почвообрабатывающих и посевных агрегатов.
Сельскохозяйственные тракторы общего назначения 5-го тягового класса предназначены для выполнения основных сельскохозяйственных работ в составе почвообрабатывающих, посевных и транспортных агрегатов. По результатам эксплуатации и лабораторно-полевых испытаний трактора К-701 с одинарными и сдвоенными колесами установлены основные рабочие передачи (1 -3,11-111 режимов) в составе почвообрабатывающих комплексов, обеспечивающие диапазон тяговых усилий от 36 до 60 кН при скоростях движения 3,3-1,7 м/с и тяговой мощности 105-120 кВт. Определяются режимы рабочего хода в основном загрузкой двигателя, тягово-сцепными свойствами трактора на основных фонах и колебаниями внешней нагрузки, параметры распределения которой соответствуют V. = 0,05-0,07 при частоте основного энергетического
спектра = 2,0 — 3,0 с-1 [1,2].
По результатам лабораторно-полевых экспериментов получены усредненные значения коэффициентов а и в уравнения регрессии, связывающего коэффициенты использования веса трактора
и буксования 5 = а Ркр при установленных значениях давления в шинах ФД-12(28,Ж26) и коэффициенте в -Ркр
сопротивления перекатывания трактора 1 на различных фонах (табл. 1).
Коэффициенты уравнения буксования, сцепления и сопротивления перекатыванию трактора К-701
Фон а в Рк max f Р пер. /зад,. МПа
Стерня 0,110 0,773 0,54 0,10 0,14/0,14
Поле, подготовленное под посев 0,086 0,640 0,52 0,16 0,14/0,13
Полученные уравнения протабулированы при различных сочетаниях фкр и 1, что позволило определить максимальные значения коэффициента сцепления рктах, соответствующие допустимому буксованию
5дтрактора, и установить графические зависимости 5 = 1(рр) на указанных фонах (рис. 1).
Источник: cyberleninka.ru
Коэффициенты запаса в практических расчетах. Объективные значения нормативных показателей надежности должны определяться для каждого отдельного вида строительных конструкций на основе глубоких
Объективные значения нормативных показателей надежности должны определяться для каждого отдельного вида строительных конструкций на основе глубоких теоретических разработок и обширных экспериментальных исследований.
В нашей стране на основе многолетней эксплуатации различных инженерных систем в зависимости от ответственности элемента, конструкции, объекта получены следующие данные нормативных значений надежности (табл. 23.1).
Значения гауссовского коэффициента надежности железобетонных конструкций, запроектированных по отечественным нормам, равны = 3. 4. Надежность, соответствующая определенным значениям следующая:
Надежность 0,9 0,99 0,999 0,9999
Значения 1,28 2,33 3,10 3,76
Таблица 23.1. Ориентировочные значения нормативной надежности
| Элемент конструкции или сооружения | Начало эксплуатации | Окончание эксплуатации |
| Малоответственный элемент конструкции | 0,90. 0,95 | 0,85. 0,90 |
| Массовый элемент статистически неопределимой конструкции, отказ которой не влечет внезапного разрушения системы | 0,99 | 0,95 |
| Ответственная конструкция (ферма, балка, колонна) с постепенными отказами | 0,999 | 0,99 |
| Ответственная конструкция с внезапными отказами | 0,9999 | 0,999 |
| Уникальное сооружение | 0,99999 | 0,9999 |
Расчеты надежности и долговечности автодорожных мостов свидетельствуют, что оптимальная надежность зависит от срока службы и Рн = 0,99. 0,999.
Оптимальное значение надежности составляет: по образованию трещины в защитном слое Рн = 0,90. 0,95; по достижении трещинами нормативной ширины раскрытия а = 0,2mm, Рн= 0,95.
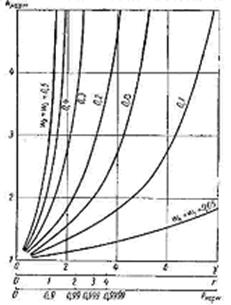
Рис. 3.4. Зависимость нормативного коэффициента запаса от нормативной надежности и от коэффициентов изменчивости при .
В инженерных нормах в качестве расчетной нагрузки принимают некоторое «максимальное» (т.е. соответствующее некоторой малой вероятности осуществления) значение, а в качестве расчетного сопротивления материала – нижнее значение из технических условий. Выбор этих значений, а также коэффициента запаса в определенной степени произволен: одной и той же надежности могут соответствовать различные коэффициенты запаса. Для того чтобы оценить величину надежности, предусматриваемой нормами, необходим статистический анализ нагрузок, сопротивлений и других параметров, влияющих на поведение конструкции [8].
Диапазоны обычно принимаемых запасов прочности при расчетах от статических нагрузок и нагрузках с небольшим числом циклов 1,5 – 2,5 и 2 — 4 при переменных нагрузках с большим числом циклов.
В строительстве, в авиастроении и других отраслях, где одним из важнейших факторов является общий вес конструкции, логично стремление к обоснованному снижению запасов прочности. Это требует уточнения не только расчетных схем, но и уточнения сведений о нагрузках, условиях работы и механических свойствах материалов. В действующих ныне строительных нормах коэффициент запаса расщепляется по типам нагрузок, неоднородности материалов и условиям работы.
При учете случайного характера всех факторов использование статистических данных часто ограничивает возможности обоснованного снижения запасов прочности всвязи с недостаточной статистикой наблюдений. Поэтому для более обоснованного назначения коэффициентов запаса в настоящее время все шире используются методы моделирования процессов и методы статистического моделирования результатов как случайных величин и случайных процессов.
Источник: studopedia.ru
IV Международная студенческая научная конференция Студенческий научный форум — 2012

АНАЛИЗ ЗНАЧЕНИЙ КОЭФФИЦИЕНТОВ ЗАПАСА ПРОЧНОСТИ ДЛЯ РАЗЛИЧНЫХ МАТЕРИАЛОВ
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Повышение надежности элементов сооружений и деталей машин предъявляет высокие требования к проектным решениям, поскольку конструкция должна быть достаточно прочной, а в необходимых случаях — жесткой и устойчивой и, вместе с тем, иметь наименьшую материалоемкость, трудоемкость изготовления и стоимость. В значительной мере эта задача может быть решена за счет рационального проектирования на основе современных методов прочностных расчетов.
Необходимость введения коэффициентов запаса прочности объясняется следующими обстоятельствами: а) разбросом в определяемых из опыта величинах σт или σв для данного материала; б) невозможностью точно установить действующие нагрузки; в) неточностью принятых методов расчета.
При назначении коэффициентов запаса, а значит и допускаемых напряжений, кроме перечисленных выше соображений необходимо также учитывать и другие факторы: а) качество и степень однородности материала, например, для стали коэффициент запаса принимается — 1,5; для бетона — 3; для естественного камня, материала весьма неоднородного, коэффициент запаса принимается ~ 10; б) долговечность и значимость сооружения или машины. Ниже представлена сравнительная таблица значений коэффициентов запаса прочности (Табл.1.), в которой можно наблюдать разброс значений этих коэффициентов.
Коэффициент запаса прочности (nт,nв)
Табличный метод выбора допускаемых напряжений и коэффициентов запаса прочности конкретней, проще и очень удобен для пользования. Поэтому во всех случаях, когда имеются специализированные таблицы допускаемых напряжений и коэффициентов запаса прочности, составленные для отдельных деталей и узлов машин научно-исследовательскими институтами, заводами и организациями, проектирующими машины, при выборе допускаемых напряжений и коэффициентов запаса обычно пользуются табличным методом. Дифференциальный метод заключается в том, что допускаемое напряжение или допускаемый коэффициент запаса прочности определяют по соответствующей формуле, которая учитывает различные факторы, влияющие на прочность рассчитываемой детали.
Коэффициенты запаса по отношению к временному сопротивлению даже при постоянных напряжениях в условиях хрупкой прочности выбираются довольно большими, например для серого чугуна порядка 3 и выше. Это связано с тем. что даже однократное превышение максимальным напряжением временного сопротивления вызывает разрушение, а для чугуна это также связано с остаточными напряжениями и неоднородной структурой.
Коэффициент запаса по отношению к пределу текучести материала при расчетах деталей из пластичных материалов под действием постоянных напряжений выбирают минимальным при достаточно точных расчетах, т.е. равным 1,3. 1,5.
Это возможно в связи с тем, что при перегрузках, превышающих предел текучести, пластические деформации весьма малы (особенно при сильно неоднородных напряженных состояниях деталей) и обычно не вызывают выхода детали из строя. Коэффициенты запаса по пределу выносливости, несмотря на опасный характер разрушения, выбирают относительно небольшими, т.е. равными1,5. 2,5.
Это связано с тем, что единичные перегрузки не приводят к разрушению. При контактных нагружениях коэффициенты запаса можно выбирать равными 1,1 . 1,3, т.к. возможные повреждения имеют местный характер.
Коэффициенты запаса можно устанавливать на основе дифференциального метода как произведение частных коэффициентов, отражающих: достоверность определения расчетных нагрузок и напряжений — коэффициент S1 = 1. 1,5; однородность механических свойств материалов — коэффициент S2; для стальных деталей из поковок и проката S2= 1,2. 1,5; для чугунных деталей S2= 1,5. 2,5; специфические требования безопасности — коэффициент S3 = 1. 1,5. Общий коэффициент запаса прочности:S = S1S2S3 [6].
Для строительных специальностей условие прочности записывается как раб σ max = . y — расчетное сопротивление (применительно к растяжению, сжатию и изгибу). Для различных напряженных состояний расчетное сопротивление определяется следующим образом: растяжение, сжатие и изгиб — Ry= Ryn/γm ; сдвиг — RS=0,58 Ryn/γm; где γm — коэффициент надежности по материалу, определяемый в соответствии с п.3.2* (СНиП II-23-81*); Ryn — нормативное сопротивление, МПа;
Расчетные сопротивления при растяжении, сжатии и изгибе листового, широкополосного универсального или фасонного проката приведены в таблице 51*, труб в табл.51,а. (СНиП II-23-81*), расчетные сопротивления гнутых профилей следует принимать равными расчетным сопротивлениям листового проката, из которого они изготовлены, при этом допускается учитывать упрочнение стали листового проката в зоне сгиба.
Для сравнительного анализа использована сталь С590. Данные, полученные при расчете с коэффициентами, взятыми из технической литературы и из СНиП II-23-81 *, сведены в табл. 2.
Источник: scienceforum.ru