Геометрия, алгебра и тригонометрия играют решающую роль в архитектурном проектировании. Архитекторы применяют эти математические формы для планирования своих чертежей или первоначальных эскизов. Они также рассчитывают вероятность проблем, с которыми может столкнуться строительная бригада, когда воплощают в жизнь проектное видение в трех измерениях.
Как математика используется в архитектуре?
Математика используется архитекторы, чтобы выразить дизайнерские образы на чертеже, чтобы, который используется строителями для создания этого изображения. … Они рисуют планы каждой части здания, включая водопроводные и электрические системы. Они также помогают выбирать строительные площадки и решать, какие материалы использовать.
Что такое математика в архитектуре?
Архитекторы используют математику по нескольким причинам, оставляя в стороне необходимость использования математики при проектировании зданий. Во-первых, они используют геометрию, потому что она определяет пространственную форму здания. Во-вторых, они использовать математику для создания форм, которые считаются красивыми или гармоничными.
Геометрия для архитектуры
Как математика встроена в здание?
Математика является основным компонентом каждой инженерной области, а также широко используется в исследованиях. В строительстве мастера используют математические концепции такие как измерение, геометрия и тригонометрия для строительства крыш или домов, штукатуры используют соотношения для смешивания составов, сантехники используют гидравлику для систем отопления.
Источник: powerpointmaniac.com
Математика в архитектуре
Математика и архитектура неразрывно связаны, ни одно современное здание не может быть рассчитано без математических формул и законов.
Архитектуру чаще всего определяют как искусство, но это понятие не дает полного представления о ее двойственной натуре. Хороший архитектор должен сочетать в себе творческое начало и инженерный ум, видеть гармонию композиции и оценивать устойчивость соединения ее элементов. И в архитектуре гораздо больше математики, чем это может показаться на первый взгляд.
Если обратиться к примерам проектирования в древние времена, то все расчеты основывались на применении пропорций и простейших математических вычислениях. Опыт показывал на практике, какие из выводов были верны, а какие нет. Здания и решения, которые доказали свою устойчивость изучались более тщательно и становились образцами для подражания, их решения многократно повторялись и совершенствовались, а успешность проекта описывалась через пропорции, математическую формулу соотношения частей и целого.
Красота архитектурных сооружений складывалась из гармонии, найденной в математических уравнениях, и являлась внешним выражением равновесия и соразмерности частей и целого.
И сегодня математика в архитектуре играет важную роль. Компьютеры, заменившие кульманы и калькуляторы на рабочих местах, автоматизировали многие расчетные операции, но не исключили их полностью. За счет мощности процессоров можно сегодня рассчитывать сложнейшие уравнения и выполнять операции, которые требовали нескольких недель труда целого коллектива.
Рисунок 1. Параметрическая архитектура. Автор24 — интернет-биржа студенческих работ
Параметрическая архитектура
Современной архитектуре свойственна одновременно и простота форм, и сложность их расчетов. За каждой линией стоит долгий процесс поиска идеальных параметров, отвечающих не только требованиям красоты, функциональности надежности, но и целям устойчивого развития, уменьшению энергопотребления.
Готовые работы на аналогичную тему
Параметризм – это новое направление в архитектуре, которое также называют стиль цифровой эпохи. В нем нашли отражение возможности вычислительной техники путем вариативного моделирования по заданному алгоритму создавать уникальные конструкции. Также к параметризму относятся все проявления вычислительного проектирования.
Следствием качественного скачка в технологиях проектирования стало появление параметрической архитектуры или параметризма, когда авторами проекта наравне с людьми выступают компьютеры и программы.
Основой этой концепции являются:
- использование алгоритмических, вычислительных комплексов;
- поиск зависимостей опирается на набор первичных условий;
- за счет варьирования миллионов возможных комбинацией параметров с определенным конечным результатом получаются уникальные параметрические конструкции.
Эта технология, использующая алгоритмы подбора параметров, позволяет не только функционально решить поставленную задачу, но и создать уникальные и идеальные для данной задачи структуры.
Примеры параметрической архитектуры мы можем встретить в работах Захи Хадид и ее бюро, помимо того, в этом направлении работают:
- бюро Crisa Santos Arquitectos;
- Powerhouse Company;
- Softroom и другие.
Рисунок 2. Центр Гейдара Алиева, Баку, архитектор Заха Хадид. Автор24 — интернет-биржа студенческих работ
Парамтерическая архитектура задала новый формат эстетики и раздвинула границы возможного. Здания перестали быть статичными и монолитными, параметрическая архитектура позволила шире взглянуть на возможности и создать устойчивые и надежные конструкции для неординарных и смелых решений. Использование математических моделей и алгоритмов, описанных задолго до развития параметризма заложило основу, на которой сегодня строится все проектирование.
Новые подходы безусловно требуют новых компетенций от архитекторов, которые должны расширить свой профессиональный кругозор и использовать более мощные и современные инструменты в работе, чтобы существенно улучшить качество и облик своих проектов. Пока мы говорим о зарождении и начале развития параметрической архитектуры, но у нее уже очень много союзников и количество реализованных проектов растет с каждым годом. За счет ее выразительности ее часто применять в авторской архитектуре, она позволяет решить проектные задачи нетривиальным путем и создать уникальный объект в соавторстве с компьютером.
Источник: spravochnick.ru
Математика в архитектуре.

Математика-это не только стройная система законов, теорем и задач, но и уникальное средство познания красоты.
Просмотр содержимого документа
«Математика в архитектуре.»
МАТЕМАТИКА В АРХИТЕКТУРЕ
Математика-это не только стройная система законов, теорем и задач, но и уникальное средство познания красоты. Многие многие матиматические теории нередко кажутся к этимпроблемам с позиции исторического развития, то станет, виден их глубокий.
Понятие «архетиктура» имеет несколько смыслов. Архетектура-древнейшая сфера человеческой деятельности («искуственного строить»- по определению Алберти) и её результат. Главный смысыл понятия архетектура состоит в том, что это совекупность заданий и сооружений различного назначения, это пространство, созданое человеком и необходимое для его жизни и деятельности.
Архетектура зарождается вместе с человечеством, сопроваждает его в историческом развити. В ней отражаются мировозрение,ценности, знания людей живших в различные исторические эпохи.В ней сосредоточены особенности культуры представителей разных национальностей. Архитектурные памятники, дошедшие до нас из глубены веков, помагают нам понять цели, взгляды, мысли, традиции и привычки, представления о красоте, уровень знаний людей, которые когда-то жили на Земле.
Для чего возводились архитектурные сооружения? Прежде всего они возводились для удобства жизни и деятельности человека.Они должны были служить его пользе: беречь его от холода и жары, дождей и палящего солнца. Они должны были зоздавать комфортные условия для различной деятельности человека- давать достаточное освещение,обеспечивать звуко изоляцию или хорошее распространение звука внутри помещения. Возводимые сооружения должны быть прочными, безопасными и долго служить людям. Но человеку свойственно ещё и стремление к красоте, поэтому всё,что он делает, он старается сделать красивым.
Архетектура- удивитель ная область человеческой деятельности. В ней тестно переплёты и строгоуровновешены наука, техника и искусство. Только соразмерно, гармоническое едиство этих начал делает возводимое человеком сооружение памитником архитектуры, неподвласным времени, подобно памитникам литературы, ваяния, музыки.Если же какой-то из элементов зодчества-наука, техника или искуство-начинает подавлять остальные, то истинная архетиктура скатывается на одно из тупиковых направлений, именуемых фукционализмом,технициолизмом,эклектизмом или ещё каким-нибудь «изломом».
Пирамиды-фантастические фигуры из камня, устрёмлённые к Солнцу. Своими громадными размерами,совершенством геометрической форммы они поражают вообраражение. Недаром эти творения рук человеческих считали одним из чудес света.
Почему из всех геометрических тел именно пирамиду выбрали древнеегипетские зодчие, для тго чтобы в веках прославить своих фаранонов? Скорее всего причина кроется в том, что такая конструкция-одна из самых устойчевых.Ведь с увеличением высоты пирамиды масса её верхней части уменьшается,а это-главный принцип надёжности постойки. Они служили символами величия и могущества фараонов, свидетельством могущества страны.
Матиматика предлагает архитектору ряд, если так можно назвать,общих правил организации частей в целое, которые помогают:
Расположить эти части в пространстве, так что в них проявляется порядок;
Установить определённое соотношение между размерами частей и задать для изменения размеров (уменьшения или увеличения)определённую единую закономерность, что обеспечивает восприятие целостности и представление о порядке;
Выделить определёное соотношение между размерами частей и задать для изменения размеров (уменьшения или увелечения) определённую единую закономерность,что обеспечивает восприятие целостности и представление о порядке;
Выдилить определённое место в пространстве, где будет размещятся сооружение, описать его определённой математической формой, которая также позволит выделить его из других сооружений и внести в их состав,создав новую компазицию,новый архитектурный ансанбль.
Возникает естественный вопрос-откуда математика черпает эти общие правила. А получает она их из природы. Главная заслуга математики состоит в том, что она выявляет глубинные свойства, которые заложены в природе, но не лежат на поверхности.
Архетектура триедина: она извечно сочетает в себе логику учёного, ремесло мастера и вдохновение художника. «Прочность, польза, красота»-такова знаменитая формула единного архетектурного целого, выведенная два тысячелетия тому назад древнегреческим теоретиком зодчества Витрувием (I в. До н. э.).Вот почему архитектура как нельзя более отвечает теме: взаимодействие математики и искусства.
Главная ценность архитектурных сооружений в их красоте. Сооружение может быть прочным и удобным, но если оно не привлекает глаз, не вызывает у нас эстетического чувства, то она воспринимается нами как обычное строение, но не как памятник архитектуры. Кроме того, архитектурное сооружение может стать непрочным и бесполезным, но при этом его архитектурная ценность не исчезнет.
Так случилось, например, со многими шедеврами древнерусского зодчества. Они были сделаны из не самого прочного материала- дерева, в связи с этим со временем стали особенно интесивно разрушаться. Во многом, благодоря этому, они перестали использоваться по своему назначению однако не перестали быть шедеврами архитектурного искуства.
В качестве примера такого сооруженния часто приводят Преоброженский собор на острове Кижи. Другими словами, без искуссва архитектуры нет. Но возникает естественный вопрос-а при чём здесь математика?
Это разнообразные геомитрические формы,пропорции и законы симметрии, которые в определённой мере задают внутрению крассоту архитектурной формы.Без неё внешние украшения зданий не улучшают, а порой усугубляют внешнее впечетление о том или ином сооружении.
Французкий зодчий, живший в XVII веке, Франсуа Блондель писал: «Удовлетворение, которое мы испытываем, глядя на прекрасное произведение искусств, проистекает от того что в нём соблюдены правила и мера, ибо удовольствия в нас вызывают единственно лишь пропорций. …Дабы подкрепить наше утверждение, я заявляю, что красота, возникающая из меры и пропорции, вовсе не требует дорогих материалов и изящной работы, дабы вызвать восхищение, напротив, она сверкает и делается все ощутимее, проступая сквозь грязь и хаос материала и его обработки». Лучшим подтверждением этих слов является скромная, не отличающаяся значительными размерами церковь Покрова Богородицы на Нерли.
Математика принимает непосредственное участие в обеспечении прочности и пользы архитектурных сооружений. Она же лежит в основе законов красоты, проявляющихся в архитектуре. Красота – внешнее выражение математических законов в архитектуре.
Для чего люди строили различные здания? Ответы на этот вопрос ясен. Прежде всего, для того, чтобы в них было удобно жить и работать. Что мы вкладываем в понятие удобства? Вспомните дом или квартиру, в которых живите вы или ваши друзья.
По каким характеристикам вы судите об их удобстве?
Достаточный внутренний объём
Хорошая звука изоляция
Как же математика может помочь в планировании помещений? Во-первых, при составлении плана чаще всего решается геометрическая задача о разбиении многоугольника на части. Во-вторых, архитектор обезательно пользуется понятием маштаб, т.к. все размеры реальных помещений он уменьшает в какое-либо одинаковое количиство раз. Он изображает план с точки зрения математики, представляя его в виде той фигуры, которую можно было бы увидеть, смотря на неё сверху. Далее математика помогает архитектуру сделать соответствущие расчёты по известным ему сспециальными формулам, чтобы решить какой толщины должны быть стены и восколько слоёв звукоизолируещего материала необхадимо проложить, чтобы обеспечит жильцам комфортные условия жизни.
Удобство для жилых помещений определяется и их планировкой. Понятно, что столовая в доме должна быть недалеко от кухни. Сейчас иногда их объединяют в единое помещение. Туалет и ванная комната должна распологаться рядом, а иногда и просто совмещяться. Наконец, спальная должна находиться рядом с ванной комнатой и туалетом. Детская комната должна быть недалеко от спальни родителей.
Вот гостиная, кабинет,библиотека могут распологаться где угодно.
Толщина стен важна не только для звукоизоляции, она обеспечивает и тепловой режим помещений. Ведь стены защищают людей от неблагоприятного воздействия окружающей среды. Ведь недаром люди говорят: «Мой дом-моя крепость».Это высказывание воспринимается в переносном смысле-как защита,крепость,прежде всего психологическая.
Но изначальный смысыл, возможно, исходил из того, что дом это защита от дождя, ветра, холода.Для нас, живущих в Сибириэто особенно важно. И в этом случае для дождя, ветра, холода. Для нас, живущих в Сибири это особенно важно. И в этом случае для обеспечения хорошей теплоизоляции нужны специальные материалы и расчёты,позволяющие обеспечитьзащитуот холода и при этом минизироватьзатраты на материалы,а значит снизить общую стоимость здания.
Итак, на примере этого плана, мы видим, что планировка моей квартиры достаточно правельная. Туалет, ванная и спальная находится рядом.Коридор играет важную функциональную роль. Он является тем пространством, объеденяющим всё входы и выходыкомнат в квартире, т.е. ни одно помещение не наблюдается у нас проходным, что очень удобно в прожевании.
В общем виде, мы видим, что квартира имеет 2 комнаты, каждая из которых имеет свой правельный размер местонахождение. Ведь понятно, что спальня или детская долны быть меньше по размеру, чем зал. Так оно у нас и есть.
Также удобство наших квартир характерезуется звукоизоляция, т.к. толщина стен не привышет среднего, которые сложены из кирпича, а значит не слишком обеспечивающие снижении уровня шума с улицы и со стороны соседей. Толщина стен важна не только для звукаизоляции, она ещё обеспечивает тепловой режим помещений, а это очень важно. Ведь стены защищают людей от неблагоприятного воздействия окружающей среды. Поэтому архитектору в построении черчежа нужно учитывать все,чтобы человеку ничто не достовляло неудобствов планировке его квартиры.
Класическая греческая архитектура (около 600-300 до н.э.). В Древней Греции архитектурное решение общественных сооружений было подчинено одной цели –достижению идеальной красоты. Около 600 до н.э. люди начали возводить здания из камня. К 490до н.э. стали строить из мрамора. Расцвет архитектуры этой эпохи отмечен такими шедеврами, как Парфеон.
Храм сооружён из пентелийского белого мрамора, со временем приобретшего тёплый желтоватый цвет. Мраморные блоки укладывались насухо и соединялись металлическими вкладышами. Даже кровля покрывалась мраморными пятисантиметровавыми плитами –“черепицей”. Древнеримская архитектура (около 200 до н.э. — 400 н.э.). Римские архитекторы заимствовали многие элементы и приемы других народов: своды у персов, арки у этрусков, множество архитектурных украшений у Греков.
Романская архитектура (1000-1100). Этот стиль хронологически следует за византийским (450-600). Для него характерно использование классических элементов, в частности круглых арочных сводок, в зданиях с толстыми стенами.
Готика(1150-1500). Отличительная черта – стрельчатые арки, занчительно увеличеть высоту высоту сводок и окон. Готика распростронилась по всей Европе и приобрила типичные узнаваемые черты.
Возрождение (1400-1600). В эпоху Возрождения руины римских сооружений стали источником вдохновения итальянских архитекторов, создавших античности. Снова в центре внимания оказались геометрические пропорции, обилие света и подленно класически декор.
Бароко и Ракоко (1600-1760). Итальянец Бернини создал пышный стиль барокко со сложным оформлением поверхностей и яркими настенными росписями.
Неокассицизм (1750-1850). В пику излишиствам и вычурности барокко некоторые европейские архитекторы, например Клод Леду , вновь обратились к античной архитектуре.
Романтизм/историзм (1800-1900). Интерес к искуству Египта и Азии, к средневековому готическому прошлому породил ряд направлений2 подражательной архитектуры.
Модерн (1890-1914). Стиль модерн охватывает архитектуру, дизайн интерера, декоротивно-приклодное искуство. Его корни следует искать в возрождении интерьера к текущим формам кельтского орнамента. Выдающимися образцами модерн сталт павильены станций Парижског метрополитена.
Ар деко (1918-1940). Для архитектуры этого направления характерны конструквитсткие формы и повторяющиеся геометрические декоротивные элементы.
Интернациональный стиль, или функциализм (1920-1975). Функциализм отвергал декоративномть и все, кроме функциального необходимого. Ле Корбузье сформулировал савои принципы архитектуры: «свободная планировка» интерера и «свободный посад»
Плюрализм (1975). Смешание разнообразных стилей, часто объедененных общим термином «постмодернизм». Школа «хай-тэк» допускает использование старых стилей в новых сочинениях. Школа «деконструкции» делаетакцент на эфекте движения и дезориентации путем зонирования пространства или, наоборот, его расширения с помощью нетродиционного потхода к таким основным элиметам, как пол и стены.
Пирамида Хиопса имеет стороны основания:230.41, 230.51, 230.60 и 230.54м. Высота равна 146.70м. Отношение наклонной образующей, или гипотенузы прямоугольного треугольника, образующего поперечный разрез пирамиды разрез пирамиды к малому катету, или половине стороны квадратного основания, равно отношению золотого сичения.
Пирамида Хефрена построена на основе отношений сторон священного египетского треугольника. Ее поперечный пвзрез определяется двумя треугольниками, сблокироваными своими большими катетами. Проверим. Сторона основания равна 215.86м, высота равна 143.65м. Архитектурные формы пирамиды Хефрена как нельзя лучше свидетельствуют об использовании, здчими Египта целочисленного треугольника 3, 4, 5. Анализ пропорций пирамид не оставляет и тени сомнения в том что зодчие древнего Египта превосходно знали и высоко ценили отношение золотого сечения.
Итак, при постройке, как современных зданий, так и зданий прошлых веков необходимы знания математики. Архитектурное формообразование с помощью геометрических построений сохраняется во всех случаях. Эта проблема стояла перед архитекторами прошлых веков, не исчезла она и сегодня.
Математика для творческого труда архитектора издавна признаётся чем-то очень важным, необходимым и плодотворным. За длительный период человеческой цивилизации создано немало произведений исключительной красоты.На языке архитектуры, можно сказать, что математика – это грандиозное мысленное сооружение. Всё сказанное убеждает нас втом, что архитектура и математика, являясь соответствующими проявлениями человеческой культуры, на протяжении веков активно влияли друг на друга.
Источник: kopilkaurokov.ru
Архитектура и математика. Математика в архитектуре

Единственный в мире Музей Смайликов
Самая яркая достопримечательность Крыма

Скачать 1.94 Mb.
«Школа с углубленным изучением отдельных предметов № 21»
«Математика в архитектуре»
ученик 10 «Б» класса
Г.о. Тольятти Самарской обл.
Акимова Марина Васильевна,
учитель МБУ «Школа № 21»
г.о. Тольятти Самарской обл.
Тольятти, 2020 г.
Проект «Математика в архитектуре» направлен на интеграцию знаний, формирование общекультурной компетентности, создание представлений о математике как науке, возникшей из потребностей человеческой практики и развивающейся из них. Ведущий подход, который был использован при разработке проекта: показать на обширном материале от античных времен до наших дней пути взаимодействия и взаимообогащения двух великих сфер человеческой культуры — науки и искусства; расширить представления о сферах применения математики; показать, что фундаментальные закономерности математики являются формообразующими в архитектуре, что архитектура и математика, являясь соответствующими проявлениями человеческой культуры, на протяжении веков активно влияли друг на друга. Они давали друг другу новые идеи и стимулы, совместно ставили и решали задачи. По сути, каждую из этих дисциплин можно рассматривать существенным и необходимым дополнением другой.
Ключевые слова: математика, геометрия, архитектура, конструкция, прочность.
Глава 1. Теоретическая часть…………………………………………..7
1.1. Математические расчеты в архитектуре.
1.2 . Взаимосвязь геометрии и архитектуры.
1.3. Прочность конструкций.
Глава 2. Практическая часть………………………………….…12
2.1. Зависимость прочности сооружений от материалов
2.1.1. Зависимость прочности сооружений от геометрической формы
2.1.2. стоечно-балочная система;
2.1.3. арочно-сводчатая конструкция
2.1.4. каркасная система
2.2.Современные Геометрические фигуры в архитектуре: однополостной гиперболоид, гиперболический параболоид
2.3. Новые геометрические формы в современной архитектуре
2.4. Создание архитектурного проекта на примере «Беседка»
Фундаментальные закономерности математики являются формообразующими в архитектуре. Знание математики – существенное и необходимое дополнение архитектуры.
Актуальность
Архитектурные объекты являются неотъемлемой частью нашей жизни. Наше настроение, мироощущение зависят от того, какие здания нас окружают. Открытие новых математических законов позволяет совершенствовать, разнообразить архитектурные формы, красоту объектов, увеличить прочность конструкций, качество строений при меньших затратах – материальных, физических, энергетических. Знание математики позволяет решать архитектурные задачи разного уровня сложности! Назрела необходимость исследования того многообразия объектов, которые появились в нашем мире! Немаловажно работать над собой, повышать свою культурную и математическую грамотность,
Практическая значимость
Материал проекта может использоваться на уроках математики, геометрии, истории и изобразительного искусства, в организации занятий внеурочной деятельности, при проведении предметных вечеров и интеллектуальных конкурсов, а также в профориентационной работе со старшеклассниками.
Объектом исследования являются архитектура зданий и пирамид.
Предметом исследования взаимосвязь архитектуры и математики.
Целью данного проекта является исследование взаимосвязи развития математики и архитектуры на практике.
Для достижения поставленной цели в работе предусматривается решение целого ряда задач:
1.Изучить литературу, интернет ресурсы о взаимосвязи математики и архитектуры
2.Убедиться в практической необходимости владения математическими знаниями в архитектуре
3.Исследовать, как геометрические формы в архитектурных стилях влияют на прочность конструкций.
4.Расширить общекультурный кругозор посредством знакомства с лучшими образцами произведений архитектуры;
5.Создать проект «Беседка»
6. Создать презентацию
Методы исследования:
1. изучение литературы и других источников информации по данной теме;
4. практическая работа.
Глава 1. Теоретическая часть
1.1. Математические расчеты в архитектуре
Архитектура – это красота. Но чтобы построить эту красоту архитекторам нужно совместить в своих творениях гармонию, удобство, экономность, красоту и долголетие, что далеко не очень просто. В этом им помогает математика. Например, при расчёте размеров помещения архитектору необходимо знать средний рост человека и формулу расчёта среднего арифметического действия.
Прежде чем начинать строительство необходимо произвести огромное количество измерений и расчётов. В России широко распространён прогрессивный метод строительства по типовым проектам, который наряду с уменьшением объема проектных работ позволяет унифицировать строительные изделия, и способствует индустриализации строительства.
Объекты, изображаемые на строительных чертежах – всевозможные здания и сооружения, состоят из отдельных частей – конструкций. При перенесении размеров земельного участка и проецировании здания архитектор пользуется признаками подобия фигур, т.е. он не чертит объект в натуральную величину, а пользуется масштабом, стандартное отношение которого 1:100. При планировке архитектор пользуется многими теоремами и аксиомами. Например, чтобы отложить несколько последовательно равных отрезков, используется знаменитая теорема Фалеса: Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
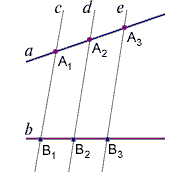
При проектировании вертикальной планировки используют графоаналитический метод: метод планирования комплекса работ, основным элементом анализа, затем и планом и документом которого является сетевой график (сетевая модель или просто сеть), представляющий собой информационную динамическую модель, в которой изображается последовательность выполнения, взаимосвязи и планируемые результаты выполнения всех работ, включённых в комплекс и необходимых для достижения заданной конечной цели разработки. После того, как все детали, элементы здания поострены, на план наносят все необходимые надписи и размеры. Итак, математические расчеты, измерения, построения – это самые важные и незаменимые методы для архитектора.
1.2 . Взаимосвязь геометрии и архитектуры.
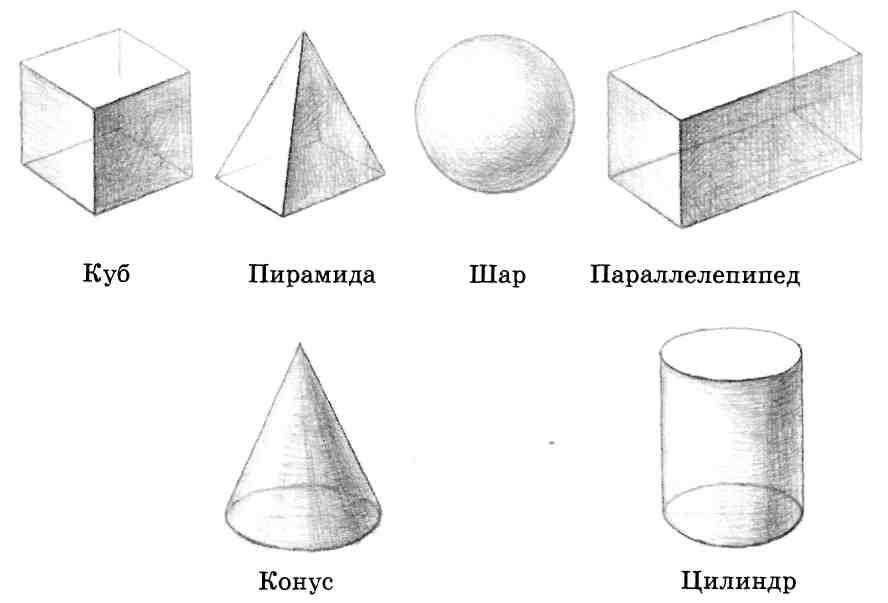
Архитектура, как вид изобразительного искусства тесно связана с геометрией. Архитектура окружает нас, формирует эстетическую городскую среду, богатую на многочисленные художественные образы. Тесная связь архитектуры и математики известна давно.
Человек всегда стремился к природе, создавая свои произведения на основе природных форм и простых геометрических фигур. «Первые архитектурные сооружения (менгиры, дольмены, обелиски, кромлехи) уже подчинялись геометрическим формам и носили религиозный характер». Произведения архитектуры являются частью пространственной структуры города. И при всем разнообразии архитектурных сооружений они почти всегда имеют в своей основе правильную геометрическую форму: призму, пирамиду, конус, шар, параллелепипед.
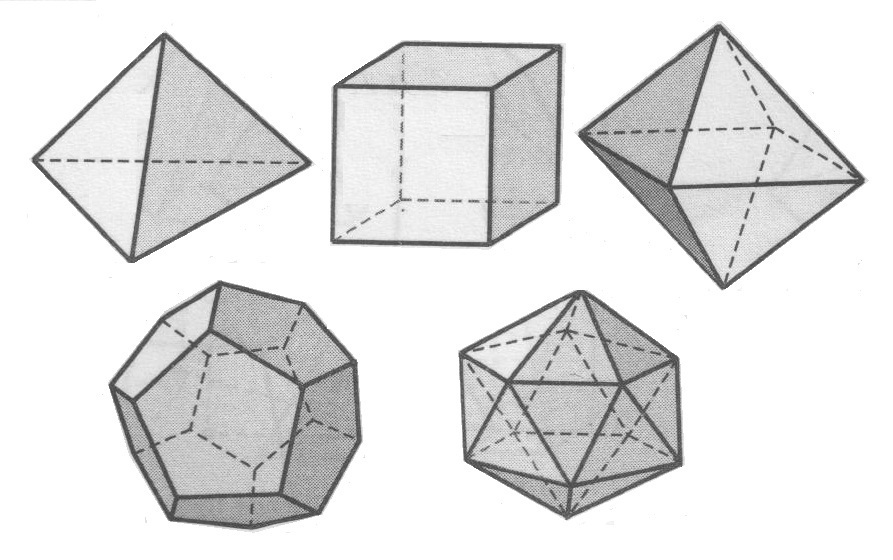
К этим формам можно добавить правильные многогранники как переходную форму между прямоугольниками и кругами.
На выбор геометрической фигуры, которая может составлять основу объемно-пространственного архитектурного сооружения, влияют такие факторы как, прочность задания, его эстетика, функциональное назначение, ассоциативность и т.п. При этом, каждая геометрическая фигура обладает своими индивидуальными свойствами.
Например, конус обладает свойством преобразования звуковой волны, проникнувшей в него. Наиболее прочной фигурой считается пирамида, так как имеет большую площадь основания. Также прочность этой форме придает уменьшение массы при увеличении высоты над уровнем земли. Формы архитектурных произведений имеют свой образный язык, воздействующий на эмоции и настроение человека.
К качественным характеристикам архитектурной формы относятся единство, целостность, равновесие, движение, соподчинение. К свойствам формы, которые влияют на эстетическую выразительность архитектурного сооружения относятся — геометрический вид, размер, цвет, фактура, светотень, расположение в пространстве, масса здания в зрительном восприятии.
Понятие архитектурной формы тесно связано с понятием архитектурной композиции, в основу которой положена определенная архитектурная идея (система построения, геометрическая форма, тема и т.д.). Геометрическая форма характеризуется размером, геометрическим строением (наличие ребер, граней, характер линии контура видимости и др.), весом, плотностью, прочностью. Кроме этого, все объемы и фасады памятников архитектуры состоят из отдельных деталей, строящиеся на базе определенного геометрического тела. Часто геометрические формы являются комбинациями различных геометрических тел.


Архитектурные стили имеют также геометрические особенности: египетский стиль — пирамиды; модернизм — призмы; постмодернизм — правильные и полуправильные многогранники; деконструктивизм — невыпуклые многогранники.
1.3. Прочность конструкций
Люди с древних времен, возводя свои жилища, думали, в первую очередь, об их прочности. Не случайно и в формуле М. Витрувия именно прочность упоминается на первом месте.
Поэтому не случайно в первом дошедшем до нас строительном кодексе, разработанном за 1800 лет до нашей эры в царствование вавилонского царя Хаммурапи, говорится: «Если строитель построил дом для человека, и дом, построенный им, обвалился и убил владельца, то строитель сей должен быть казнен». Известен и такой факт, что архитектор, создавший проект моста, в прежние времена должен был стоять под ним, когда мост открывался и по нему ехал первый транспорт.
В случае если он оказывался не прочным, т. е. он не выдерживал тех нагрузок, на которые был рассчитан, то его создатель должен быть первым, кто поплатиться за свою ошибку жизнью. Становится ясно, что прочность сооружений была связана с безопасностью людей, которые ими пользовались. Прочность связана и с долговечностью.
На возведение зданий люди тратили огромные усилия, а значит, были заинтересованы в том, чтобы они простояли как можно дольше. Кстати, благодаря этому, до наших дней дошли и древнегреческий Парфенон, и древнеримский Колизей. Оставив в стороне этическую сторону описанных деяний, остановимся теперь на вопросе о том, отчего же зависит прочность сооружения.
Глава 2. Практическая часть
2.1 Зависимость прочности сооружений от материалов.
Первым, что приходит на ум, это толщина стен. Сразу оживает сцена взятия крепости, будь то Древняя Русь или Средневековая Европа. Толщина стен этих сооружений соотносилась с пробивными возможностями орудий, которые использовались при штурме. Но еще важнее для обеспечения прочности сооружений особенности тех материалов, из которых они построены.
Вспомним в связи с этим хотя бы сказку о трех поросятах. Традиционным строительным материалом на земле является камень – гранит, мрамор, песчаник и другие. В России, богатой лесами, большинство зданий первоначально строились из дерева.
Достаточно вспомнить образцы древнерусского деревянного зодчества на острове Кижи или в музеях под открытым небом под Архангельском и Костромой. Можно вспомнить в этой связи, что в древних Китае и Японии, например, был весьма распространен бамбук в качестве строительного материала.
Очевидно, что люди для строительства своих жилищ использовали, в первую очередь, тот материал, который был под рукой. Однако это не означало, что он был наиболее прочным. Самым прочным строительным материалом всегда был камень. Он обладал еще рядом замечательных свойств, которые делали его предпочтительным строительным материалом.
С развитием промышленного производства у человека появились возможности создавать самому новые строительные материалы, которые, с одной стороны, были похожи на камень, а, с другой, превосходили его в ряде характеристик, тем самым, обеспечивая прочность сооружений. К ним относятся кирпич, металл (в первую очередь, железо) и, наконец, железобетон.
В современной архитектуре широко используются материалы, которые раньше или просто не существовали, или были слишком дороги в производстве. К таким материалам относится пластмасса, стекло. В последнее время все более широкое применение при создании архитектурных сооружений стал занимать титан. Многие специалисты считают, что титан это металл для будущих архитектурных сооружений, которые люди будут возводить, возможно, не только на Земле, но и на других планетах.
2.1.1 Зависимость прочности сооружений от геометрической формы
Но прочность сооружения обеспечивается не только материалом, из которого оно создано, но и конструкцией, которая используется в качестве основы при его проектировании и строительстве. Прочность архитектурных сооружений, важнейшее их качество.
Связывая прочность, во-первых, с теми материалами, из которых они созданы, а, во-вторых, с особенностями конструктивных решений, оказывается, прочность сооружения напрямую связана с той геометрической формой, которая является для него базовой. Математик бы сказал, что здесь очень важна геометрическая форма (тело), в которое вписывается сооружение.
Говоря о вписанности архитектурного сооружения в определенное геометрическое тело, обычно отступают от точного геометрического представления об этом понятии. Речь идет о том, что архитектурное сооружение можно представить как помещенное в определенное геометрическое тело, как можно ближе к его границам.
Другими словами, речь идет о той геометрической фигуре, которая может рассматриваться как модель соответствующей архитектурной формы. Оказывается, что геометрическая форма также определяет прочность архитектурного сооружения. Самым прочным архитектурным сооружением с давних времен считаются египетские пирамиды.
Как известно они имеют форму правильных четырехугольных пирамид. Именно эта геометрическая форма обеспечивает наибольшую устойчивость за счет большой площади основания. С другой стороны, форма пирамиды обеспечивает уменьшение массы по мере увеличения высоты над землей. Именно эти два свойства делают пирамиду устойчивой, а значит и прочной в условиях земного тяготения.
«Рациональность» геометрической формы пирамиды, которая позволяет выбирать и внушительные размеры для этого сооружения, придает пирамиде величие, вызывает ощущение вечности и внушительности.
2.1.2 . Стоечно-балочная система
На смену пирамидам пришла стоечно-балочная система. С точки зрения геометрии она представляет собой многогранник, который получится, если мысленно на два вертикально стоящих прямоугольных параллелепипеда поставить еще один прямоугольный параллелепипед.

Это одна из первых конструкций, которая стала использоваться при возведении зданий и представляет собой сооружения, которые состоят из вертикальных стоек и покрывающих их горизонтальных балок. Первым таким сооружением было культовое сооружение – дольмен. Оно состояло из двух вертикально поставленных камней, на которые был поставлен третий вертикальный камень.
Назначение этого культового сооружения до сих пор неясно. Однако в нем воплощена идея преодоления человеком силы притяжения. Кроме дольмена, до нас дошло еще одно сооружение, представляющее простейшую стоечно-балочную конструкцию – кромлех.
Это также культовое сооружение, предположительно предназначенное для жертвоприношений и ритуальных торжеств. Кромлех состоял из отдельно стоящих камней, которые накрывались горизонтальными камнями. При этом они образовывали две или несколько концентрических окружностей. Самый знаменитый кромлех сохранился до наших дней в местечке Стоунхендж в Англии.
Некоторые ученые считают, что он был древней астрономической обсерваторией. Сегодня это сооружение связывают с посещением Земли инопланетянами. Нужно заметить, что до сих пор стоечно-балочная конструкция является наиболее распространенной в строительстве. Большинство современных жилых домов в своей основе имеют именно стоечно-балочную конструкцию.
Камень, из которого возводились сооружения на основе стоечно-балочной конструкции, плохо гнется, он обычно разрушается под действием своего собственного веса. Поэтому под балки нужно было ставить достаточно много стоек. Их делали в виде колонн различного вида. Для того чтобы украсить здание такие колонны облачали в формы кариатид или атлантов.

Камень плохо работает на изгиб, но хорошо работает на сжатие. Это привело к использованию в архитектуре арок и сводов. Так возникла новая арочно-сводчатая конструкция.
2.1.3. Арочно-сводчатая конструкция.
С появлением арочно-сводчатой конструкции в архитектуру прямых линий и плоскостей, вошли окружности, круги, сферы и круговые цилиндры. Первоначально в архитектуре использовались только полуциркульные арки или полусферические купола. Это означает, что граница арки представляла собой полуокружность, а купол – половину сферы.
Например, именно полусферический купол имеет Пантеон – храм всех богов — в Риме. Диаметр купола составляет 43 м. При этом высота стен Пантеона равна радиусу полусферы купола. В связи с этим получается, что само здание этого храма как бы «накинуто» на шар диаметром 43 м. Этот вид конструкции был наиболее популярен в древнеримской архитектуре.
Арочно-сводчатая конструкция позволяла древнеримским архитекторам возводить гигантские сооружения из камня. К ним относится знаменитый Колизей или амфитеатр Флавиев. Свое название он получил от латинского слова colosseus, которое переводится как колоссальный, или огромный.
Эта же конструкция использовалась при создании гигантских терм (бань) Каракаллы и Диоклетиана, вмещавших одновременно до 3 тысяч посетителей. Сюда же следует отнести и систему арочных водоводов-акведуков, общая протяженность которых составляла 60 км.
Всем была хороша арочно-сводчатая конструкция, но она имела один недостаток – слишком большая сила действовала в основании арок (сводов) наклонно вбок (в отличие от стоечно-балочной конструкции, где сила тяжести действует вертикально). Эти боковые усилия, которые архитекторы называют боковым распором, требуют большой толщины стен, которая должна гасить эти усилия. Так, например, толщина стен Пантеона в Риме, поддерживающих купол, равна 7 метрам. Это требовало большого расхода материалов. Следующим этапом развития архитектурных конструкций явилась каркасная система, которая в основном используется в современной архитектуре.
2.1.4. Каркасная система
Прообразом ее стала разновидность арочно-сводчатой конструкции, содержащей стрельчатые арки. На смену полуциркульным аркам приходят стрельчатые, которые с точки зрения геометрии являются более сложными. Стрельчатую арку нельзя построить одним движением циркуля. Рассмотрим один из способов построения схематического изображения стрельчатой арки.
Стрельчатая арка состоит из двух дуг окружности одного радиуса. Значит, необходимо выбрать определенный раствор циркуля и закрепить его. Затем провести горизонтальную прямую. В любую точку этой прямой поставить ножку циркуля и провести дугу (можно полуокружность).
Затем ножку циркуля поставить на горизонтальную прямую так, чтобы она оказалась со стороны выпуклой части уже построенной дуги, и снова провести дугу тем же радиусом. Две дуги пересекутся. Над горизонтальной линией мы получили схематическое изображение стрельчатой арки.
Стрельчатые своды выполнялись не как монолитные, а состоящие из частей – распалубок. Каждая распалубка выполнялась на каменных ребрах, называемых нервюрами. Нервюры являются подобием скелета свода, которые принимает на себя основную нагрузку.

Боковой распор от стрельчатых арок гасился вне стен, несущих свод. Для этого вне сооружения ставились специальные опоры – контрфорсы, нагрузка на которые передавалась с помощью арочных конструкций – аркбутанов. Аркбутаны как раз и являлись тем каркасом, которые окружал сооружение и принимал на себя основные нагрузки.
Арочная конструкция послужила прототипом каркасной конструкции, которая сегодня используется в качестве основной при возведении современных сооружений из металла, стекла и бетона. Достаточно вспомнить конструкции известных башен: Эйфелевой башни в Париже и телебашни на Шаболовке. Телебашня на Шаболовке состоит из нескольких поставленных друг на друга частей однополостных гиперболоидов. Причем каждая часть сделана из двух семейств прямолинейных балок.

2.2.Современные Геометрические фигуры в архитектуре: однополостной гиперболоид, гиперболический параболоид
Прежде всего, разберемся, какая геометрическая фигура называется однополостным гиперболоидом. Само слово гиперболоид может быть знакомо по названию фантастического романа «Гиперболоид инженера Гарина». Однако, что это за геометрическая фигура, какими свойствами она обладает? Однополостный гиперболоид – это поверхность, образованная вращением в пространстве гиперболы, расположенной симметрично относительно одной из осей координат в прямоугольной системе координат, вокруг другой оси. На рисунке, который изображен ниже, выделена гипербола, которая симметрична относительно оси у, а вращается она относительно оси z.
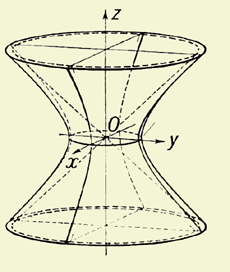
Таким образом, мы получили гиперболоид, который называется однополостным. Обратите внимание, что любое осевое сечение однополостного гиперболоида будет ограничено двумя гиперболами. Другой интересной для архитекторов геометрической поверхностью оказался гиперболический параболоид. Это поверхность, которая в сечении имеет параболы и гиперболу.
На рисунке изображен гиперболический параболоид. Именно его архитекторы кратко называют гипар.
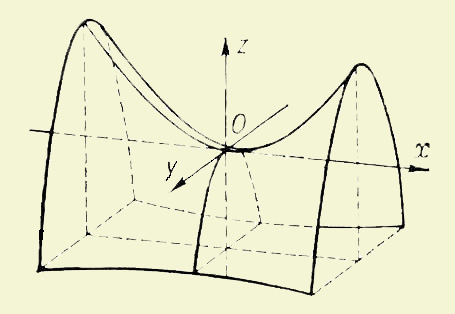
Почему эти геометрические фигуры оказались интересными для современных архитекторов? Дело в том, что они обладают одним очень важным с практической точки зрения свойством. Не являясь плоскими, они могут быть, в то же время, построены с помощью прямых линий. А это очень важно при строительстве различных сооружений из железобетона.
Чтобы придать этому материалу нужную форму изготавливают опалубку (форму), которую делают из прямых досок. Поэтому так важно, чтобы поверхность можно было образовать с помощью прямых линий. Самые простые неплоские поверхности – цилиндрическая и коническая — можно построить с помощью прямых. Это хорошо видно на рисунке.
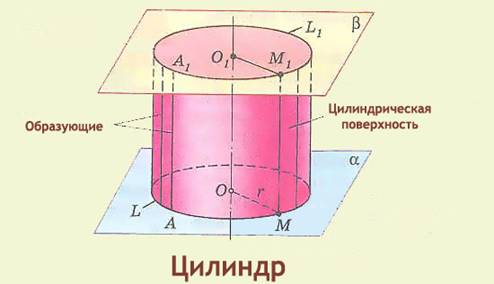
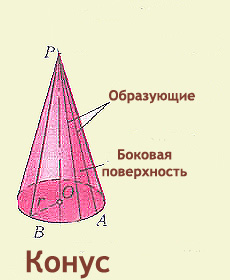
В первом случае, если речь идет о прямом круговом цилиндре, то прямая должна перемещаться параллельно в пространстве и проходить через все точки окружности, лежащей в плоскости, перпендикулярной этой прямой. Во втором случае прямая должна также проходить через все точки окружности и через одну точку в пространстве, не лежащей в плоскости окружности. Однополостный гиперболоид и гиперболический параболоид образованы перемещением не одной, а двух прямых. Иногда говорят, что они образованы семействами двух прямых. Свойство поверхностей, состоящее в том, что они могут быть образованы прямыми, называется линейчатым, а сами поверхности также носят название линейчатых.
2.3. Новые геометрические формы в современной архитектуре.
Появление новых строительных материалов делает возможным создание тонкого железобетонного каркаса и стен из стекла. Достаточно вспомнить американские небоскребы или, например, здание Кремлевского дворца съездов созданных из стекла и бетона. Именно эти материалы и каркасные конструкции стали преобладающими в архитектурных сооружениях XX века.
Они обеспечивают зданиям высокую степень прочности. С давних времен и до наших дней эталоном прочности для архитекторов являлась скорлупа куриного яйца. Отношение диаметра куриного яйца к толщине его скорлупы в среднем равно 130. Такое соотношение между диаметром пролета и его толщиной в сооружениях из камня было невозможно.
Например, это отношение для купола Флорентийского собора, выполненного из камня и кирпича равнялось 11. Но для железобетонных сводов это отношение сегодня может достигать 1800, т. е. почти в 15 раз превосходить показатель, характеризующий прочность яичной скорлупы.
2.4. Создание архитектурного проекта на примере «Беседка»
III. Выводы по работе. Рефлексия .
В ходе исследовательской работы выяснилось, что при постройке, как современных зданий, так и зданий прошлых веков необходимы знания математики – это означает, что работа имела положительный результат. За время работы над проектом я научился различать виды конструкции зданий, а так же создавать план-чертёж небольших построек. В самом начале работы над проектом, кто бы мог подумать, что я заинтересуюсь этой темой, займусь самообразованием и сам захочу углубиться в изучение развития архитектуры и математики.
Библиографический список
1.Литература и интернет ресурсы 2. 3
Бартенев И. А. Форма и конструкция в архитектуре. – Л.: Стройиздат, 1968.
Кащенко . Геометрия. Архитектура. – 2-е изд. перераб. и доп. – Киев: Будивельник, 1988.
Источник: topuch.ru