Документ из архива «Метод конечных элементов (МКЭ)», который расположен в категории » «. Всё это находится в предмете «строительная механика» из раздела «», которые можно найти в файловом архиве МГТУ им. Н.Э.Баумана. Не смотря на прямую связь этого архива с МГТУ им. Н.Э.Баумана, его также можно найти и в других разделах. Архив можно найти в разделе «книги и методические указания», в предмете «строительная механика» в общих файлах.
Онлайн просмотр документа «Метод конечных элементов (МКЭ)»
Текст из документа «Метод конечных элементов (МКЭ)»
Основные понятия и определения. Общая схема метода.
Метод конечных элементов (МКЭ) — основной метод современной строительной механики, лежащий в основе подавляющего большинства современных программных комплексов, предназначенных для выполнения расчетов строительных конструкций на ЭВМ. МКЭ также используется для решения других разнообразных задач как в области прочностных расчетов, так и во многих других сферах, например задачах гидродинамики, электромагнетизма, теплопроводности и многих других.
Метод конечных элементов (FEM) vs метод контрольного объёма (FVM). В чём разница?
Метод конечных элементов позволяет практически полностью автоматизировать расчет стержневых систем, хотя, как правило, требует выполнения значительно большего числа вычислительных операций по сравнению с классическими методами строительной механики. Однако, в современных условиях большой объем вычислений не является серьезной проблемой, и, в связи с этим, при внедрении ЭВМ в инженерную практику МКЭ получил широчайшее распространение 1 . Поэтому, знание основ метода конечных элементов и современных программных средств, позволяющих на его основе решать разнообразные задачи, в наше время для инженера является абсолютно необходимым.
В МКЭ стержневая система мысленно разбивается на отдельные части — конечные элементы, соединяющиеся между собой в узлах (рис.1). Узлы могут быть жесткими и шарнирными. Совокупность соединенных между собой и прикрепленных к основанию конечных элементов образует расчетную схему метода, называемую конечно-элементной схемой или конечно-элементной моделью или просто системой элементов. Элементы и узлы конечно-элементной схемы нумеруются.
Внешняя нагрузка считается приложенной только в узлах конечно-элементной схемы. В общем случае переход от заданной нагрузки к узловой осуществляется следующим образом. На основании принципа суперпозиций рассматриваемое состояние стержневой системы может быть представлено как сумма двух состояний (рис.2).
В первом состоянии (задача1) вводятся связи, препятствующие всем возможным смещениям узлов системы, аналогично тому, как образуется основная система в методе перемещений. При этом, однако, продольными деформациями стержней не пренебрегают. От действия заданных нагрузок во введенных связях возникают реакции.
Во втором состоянии (задача 2) узлы конечно-элементной схемы не закреплены от смещений, но к ним прикладываются усилия равные по модулю реакциям в связях, определенным в первом состоянии, но противоположные им по направлению (рис.2). Расчет системы в первом состоянии не представляет труда. В частности, если конечно-элементная схема создается таким образом, чтобы элементы представляли собой отдельные стержни (элементы 1, 2 и 3 на рис.2), то для каждого из таких элементов имеется табличное решение (таблица 11.1), позволяющее определить реакции в связях и построить эпюры внутренних усилий по их длине. Для расчета же системы во втором состоянии, т.е. для решения задачи 2, и применяется метод конечных элементов. Окончательное решение задачи будет представлять собой сумму решений этих двух задач.
Основы метода конечных элементов. Часть 1. Идея МКЭ в задачах конструкционного анализа
В задаче 2 усилия, действующие на любой элемент приложены исключительно в узлах. В этом случае перемещения узлов любого элемента, взятого в отдельности (рис.3), однозначно определяют усилия и перемещения в любой точке этого элемента. Как известно, для стержневых систем решение такой задачи может быть найдено точно.
Каждый, взятый отдельно от системы, конечный элемент должен быть достаточно простым, чтобы имелась возможность легко определить перемещения и усилия в любом сечении стержней элемента по заданным перемещениям его узлов. Связь между перемещениями узлов элемента и усилиями в них задается при помощи матрицы жесткости элемента. Количество перемещений узлов элемента, которые однозначно определяют состояние данного элемента называют числом степеней свободы элемента. Оно определяется по формуле:
где -число шарнирных узлов в элементе, а — число жестких узлов в элементе. Действительно, если узел представляет собой шарнир, то его положение на плоскости можно охарактеризовать двумя линейными перемещениями, например в вертикальном и горизонтальном направлениях. В случае жесткого узла необходимо еще дополнительно к линейным смещениям задать его поворот.
На рис.4 первый элемент имеет характеризуется четырьмя степенями свободы, т.к. он содержит два шарнирных узла. При отсутствии нагрузки, кроме приложенной в самих узлах, положение на плоскости любой точки этого элемента определяется четырьмя параметрами — двумя вертикальными и двумя горизонтальными перемещениями узлов элемента. У второго элемента на рис.4 — пять степеней свободы — к четырем линейным смещениям добавляется поворот в одном из узлов. У третьего элемента — шесть степеней свободы, которым соответствуют четыре линейных и два угловых перемещения.
Аналогично, для всей конечно-элементной схемы вводятся матрица жесткости системы или глобальная матрица жесткости, устанавливающая связь между перемещениями узлов системы и усилиями в них, а также число степеней свободы системы или глобальное число степеней свободы — количество перемещений узлов системы, которые достаточно знать, чтобы однозначно определить состояние всей системы. Оно также определяется по формуле (1), в которой -число шарнирных узлов, а — число жестких узлов во всей конечно-элементной схеме.
Например, при расчете методом конечных элементов висячей системы, приведенной на рис.х.10, может использоваться конечно-элементная схема, изображенная на рис.5. Она содержит в себе 28 шарнирных узлов, следовательно характеризуется 56 степенями свободы.
В конечно-элементной схеме балки (рис.6) используется один жесткий и три шарнирных узла. Следовательно, в соответствии с (1) эта схема характеризуется 32+13=9 степенями свободы.
Для всех элементов, из которых состоит конечно-элементная схема, должны быть построены матрицы жесткости элементов. В программных комплексах, реализующих алгоритм метода конечных элементов, хранятся готовые матрицы жесткости для элементов различных типов.
На практике, при расчете плоских стержневых систем используют готовые матрицы жесткости для элементов только трех типов: простых стержней с двумя жесткими узлами, двумя шарнирными узлами, одним жестким и одним шарнирным узлом (рис.4). В этом случае при разбивке стержневой системы на элементы узлы вводятся в местах соединения и изломов стержней, в опорах, шарнирах и на свободных концах консольных стержней. В принципе узел может быть введен и в любых других точках, например, в точках приложения сосредоточенных сил..
В учебных целях могут использоваться и элементы других типов (рис.7), в том числе и включающие в себя опорные закрепления.
Из построенных матриц жесткости элементов формируется матрица жесткости системы. Для этого все матрицы жесткости элементов и матрица жесткости системы должны быть сформированы в единой системе осей координат, называемой глобальной системой осей координат. При расчете плоских стержневых систем традиционно используется следующая глобальная система осей координат (рис.8): ось1 направлена вправо, ось 2 — вверх, ось 3 — против часовой стрелки.
Матрицы жесткости элементов могут формироваться и храниться в памяти ЭВМ в своих, локальных системах осей координат, в общем случае отличных от глобальной системы осей координат. В данной ситуации при помощи специальной процедуры эти матрицы должны быть перестроены для глобальной системы осей координат.
Так как матрица жесткости системы устанавливает связь между усилиями, приложенными к ее узлам и перемещениями ее узлов, то имея построенную матрицу жесткости системы и зная внешнюю узловую нагрузку, можно найти перемещения всех узлов конечно-элементной схемы. Для этого требуется решить систему линейных алгебраических уравнений. Порядок этой системы равен числу ее степеней свободы.
По известным перемещениям узлов системы для каждого элемента при помощи имеющихся матриц жесткости элементов можно найти внутренние усилия в элементах от действия нагрузки, приложенной в узлах (задача 2). Окончательное решение задачи, как уже упоминалось, ищется как сумма решений задачи 1 и задачи 2.
Таким образом, метод конечных элементов в данном виде аналогичен методу перемещений, так как сначала определяются перемещения узлов системы, а затем по ним — деформации и усилия в стержнях. Возможна реализация метода конечных элементов и в форме метода сил, однако она имеет ряд существенных недостатков и поэтому представляет большей частью чисто научный, но не практический интерес.
Итак, расчет стержневой системы методом конечных элементов в форме метода перемещений состоит из следующих этапов:
Создание конечно-элементной схемы (разбивка системы на элементы и их нумерация).
Сведение заданной внешней нагрузки к узловой.
Формирование матриц жесткости всех элементов системы в локальных системах координат и их преобразование в глобальную систему координат.
Формирование глобальной матрицы жесткости, системы уравнений метода конечных элементов и ее решение.
Определение усилий в элементах от действия узловой нагрузки.
Определение окончательных значений усилий в элементах путем сложения решений задач 1 и 2.
Далее подробно рассмотрим все эти этапы.
Конечный элемент. Матрица жесткости конечного элемента.
Рассмотрим произвольный конечный элемент с числом степеней свободы nст.
Вектором узловых перемещений конечного элемента называется вектор, складывающийся из значений перемещений его узлов по направлению всех его степеней свободы. Очевидно, размерность вектора узловых перемещений равна числу степеней свободы элемента nст.

Например, для двухузлового элемента, имеющего в конечно-элементной схеме номер 7, характеризующегося тремя степенями свободы (рис.9), вектор узловых перемещений будет иметь следующий вид: .
Здесь введены следующие обозначения: — перемещение узла k по направлению j, -вектор узловых перемещений узла е. Понятно, что если узел k шарнирный, то j может быть равно 1 или 2. Если же узел k жесткий, то j может быть равно 1, 2 или 3.
Аналогично вводится вектор узловых усилий, действующих на элемент. Его компонентами являются усилия, приложенные к элементу в узлах и действующие по направлению всех его степеней свободы. Для приведенного на рис.9 элемента этот вектор будет иметь вид (рис.10):
Источник: studizba.com
Метод конечных элементов в строительной механике — Finite element method in structural mechanics
Метод конечных элементов (МКЭ) — это мощный метод, изначально разработанный для численного решения сложных задач строительной механики , и он остается методом выбора для сложных систем. В FEM структурная система моделируется набором соответствующих конечных элементов, соединенных между собой в дискретных точках, называемых узлами. Элементы могут иметь такие физические свойства, как толщина, коэффициент теплового расширения , плотность , модуль Юнга , модуль сдвига и коэффициент Пуассона .
История
Происхождение конечного метода можно проследить до матричного анализа конструкций, в котором было введено понятие матричного подхода смещения или жесткости. Концепции конечных элементов были разработаны на основе инженерных методов в 1950-х годах. Метод конечных элементов получил свой настоящий импульс в 1960-х и 1970-х годах Джоном Аргирисом и его сотрудниками; в Штутгартском университете — Рэй В. Клаф ; в Калифорнийском университете в Беркли — Ольгерд Зенкевич и его сотрудники Эрнест Хинтон , Брюс Айронс ; в Университете Суонси — Филипп Ж. Чиарле ; в Парижском университете ; в Корнельском университете , Ричард Галлахер и его сотрудники. Оригинальные работы, такие как работы Аргириса и Клафа, стали основой современных методов структурного анализа методом конечных элементов.
Прямые или изогнутые одномерные элементы с такими физическими свойствами, как осевая жесткость, жесткость на изгиб и скручивание. Этот тип элементов подходит для моделирования кабелей, раскосов, ферм, балок, ребер жесткости, решеток и рам. Прямые элементы обычно имеют два узла, по одному на каждом конце, в то время как для изогнутых элементов потребуется не менее трех узлов, включая конечные узлы. Элементы располагаются на центральной оси фактических стержней.
- Двумерные элементы, которые сопротивляются только силам в плоскости за счет действия мембраны (плоское напряжение , плоская деформация ), и пластины, которые сопротивляются поперечным нагрузкам за счет поперечного сдвига и изгиба (пластины и оболочки ). Они могут иметь различную форму, например плоские или изогнутые треугольники и четырехугольники . Узлы обычно размещаются по углам элемента, и, если требуется для большей точности, дополнительные узлы могут быть размещены по краям элемента или даже внутри элемента. Элементы располагаются посередине фактической толщины слоя.
- Элементы в форме тора для осесимметричных задач, таких как мембраны, толстые пластины, оболочки и твердые тела. Сечение элементов аналогично описанным ранее типам: одномерное для тонких пластин и оболочек и двумерное для твердых тел, толстых пластин и оболочек.
- Трехмерные элементы для моделирования трехмерных тел, таких как детали машин , плотины , насыпи или массивы грунта. Общие формы элементов включают тетраэдры и шестигранники . Узлы размещаются в вершинах и, возможно, на гранях элемента или внутри элемента.
Взаимосвязь и перемещение элементов
Элементы связаны между собой только на внешних узлах, и вместе они должны максимально точно охватывать всю область. Узлы будут иметь узловые (векторные) смещения или степени свободы, которые могут включать смещения , вращения и, для специальных приложений, производные смещений более высокого порядка . Когда узлы смещаются, они будут тащить элементы определенным образом, определенным формулировкой элемента. Другими словами, перемещения любых точек в элементе будут интерполированы из узловых перемещений, и это основная причина приближенного характера решения.
Практические соображения
С точки зрения приложения важно смоделировать систему таким образом, чтобы:
- Условия симметрии или антисимметрии используются для уменьшения размера модели.
- Совместимость смещения, включая любую требуемую неоднородность, обеспечивается в узлах и, предпочтительно, также по краям элементов, особенно когда соседние элементы имеют разные типы, материал или толщину. Совместимость перемещений многих узлов обычно может быть наложена через отношения ограничений.
- Поведение элементов должно отражать доминирующие действия реальной системы как на местном, так и на глобальном уровне.
- Сетка элемента должна быть достаточно мелкой для обеспечения приемлемой точности. Для оценки точности сетка уточняется до тех пор, пока важные результаты не покажут небольших изменений. Для большей точности соотношение сторон элементов должно быть как можно ближе к единице, а элементы меньшего размера должны использоваться над частями с более высоким градиентом напряжения .
- Надлежащие опорные ограничения накладываются с особым вниманием к узлам на осях симметрии.
Крупномасштабные коммерческие программные пакеты часто предоставляют средства для создания сетки и графического отображения входных и выходных данных, что значительно облегчает проверку как входных данных, так и интерпретацию результатов.
Теоретический обзор формулировки смещения МКЭ: от элементов к системе, к решению
Хотя теория МКЭ может быть представлена в различных ракурсах или акцентах, ее развитие для структурного анализа следует более традиционному подходу с использованием принципа виртуальной работы или принципа минимальной полной потенциальной энергии . Виртуальный работа подход принцип носит более общий характер, как это применимо к линейному и нелинейному материалу поведению. Метод виртуальной работы является выражением сохранения энергии : для консервативных систем работа, добавленная к системе набором приложенных сил, равна энергии, запасенной в системе в виде энергии деформации компонентов конструкции.
Принцип виртуальных перемещений структурной системы выражает математическое тождество внешней и внутренней виртуальной работы:
Другими словами, сумма работы, совершенной над системой набором внешних сил, равна работе, накопленной в виде энергии деформации в элементах, составляющих систему.
Виртуальную внутреннюю работу в правой части приведенного выше уравнения можно найти, суммируя виртуальную работу, проделанную над отдельными элементами. Последнее требует использования функций «сила-смещение», которые описывают реакцию для каждого отдельного элемента. Следовательно, смещение структуры описывается коллективной реакцией отдельных (дискретных) элементов. Уравнения записываются только для небольшой области отдельных элементов конструкции, а не для одного уравнения, описывающего реакцию системы в целом (континуум). Последнее привело бы к неразрешимой проблеме, отсюда и полезность метода конечных элементов. Как показано в следующих разделах, уравнение ( 1 ) приводит к следующему основному уравнению равновесия для системы:
Источник: ru.abcdef.wiki
Расчет на прочность методом конечных элементов
Расчет на прочность — обязательное условие при проектировании и изготовлении ответственных изделий. Важно знать, как поведет себя деталь в реальных условиях эксплуатации под воздействием всех нагрузок.
Определить выдержит ли изделие условия эксплуатации можно на натурном образце экспериментальным способом при проведении испытаний, но не всегда у разработчика есть такая возможность. Иногда изготовление детали является слишком дорогостоящим, занимает много времени или сложно смоделировать нагрузку, в таких случаях инженеру приходит на помощь метод конечных элементов.
Суть метода конечных элементов
Метод конечных элементов — способ представления непрерывного тела с помощью большого количества элементов конечно малого размера. Такой способ упрощает существующую модель, за счет этого даёт возможность произвести все необходимые расчеты с помощью компьютера, при этом результаты имеют лишь небольшое отклонение от реальных данных.
Сама геометрия детали разбивается на малые треугольники, в зависимости от их расположения они могут иметь разные размеры. Таким образом мы сводим дифференциальную задачу к системе уравнений для заданных точек, связанных друг с другом. Чем на более мелкие элементы мы разобьем исследуемую модель, тем с большей точностью получим результаты расчета.
Задача расчета на прочность методом конечных элементов решается специализированными инженерными программами. В настоящий момент их есть большое множество. Некоторые программы универсальны, некоторые рассчитаны на определенные виды расчетов.
Инженером данная задача решается заданием твердотельной 3D модели правильных граничных условий, разбивкой модели на конечные элементы с учетом предполагаемых проблемных мест. Далее программа выполняет все необходимые расчеты. Процесс компьютерной симуляции требует большое количество системных ресурсов и времени работы, поэтому выполнять эти работы желательно на мощных компьютерах.
Последним этапом является анализ полученных компьютерных данных, установление слабых мест в конструкции и решение с помощью изменения геометрии или подбора материала.
Источник: tech-structure.ru
Расчеты на прочность в автомобильной промышленности методом конечных элементов
Расчеты методом конечных элементов (МКЭ) уже без малого век одинаково успешно применяются во всех отраслях промышленности. Метод конечных элементов возник из необходимости решения задач строительной механики и теории упругости в 1930-х годах, то есть задолго до появления мощных электронно-вычислительных машин. Основоположниками идей, лежащих в основе МКЭ, являются Александр Павлович Хренников и Рихард Курант. Сегодня я расскажу о применении МКЭ в XXI веке – на примере современных проектов в автомобильной промышленности: автотранспортера (автовоза), грузовой эстакады, легкового автомобиля и внедорожника.
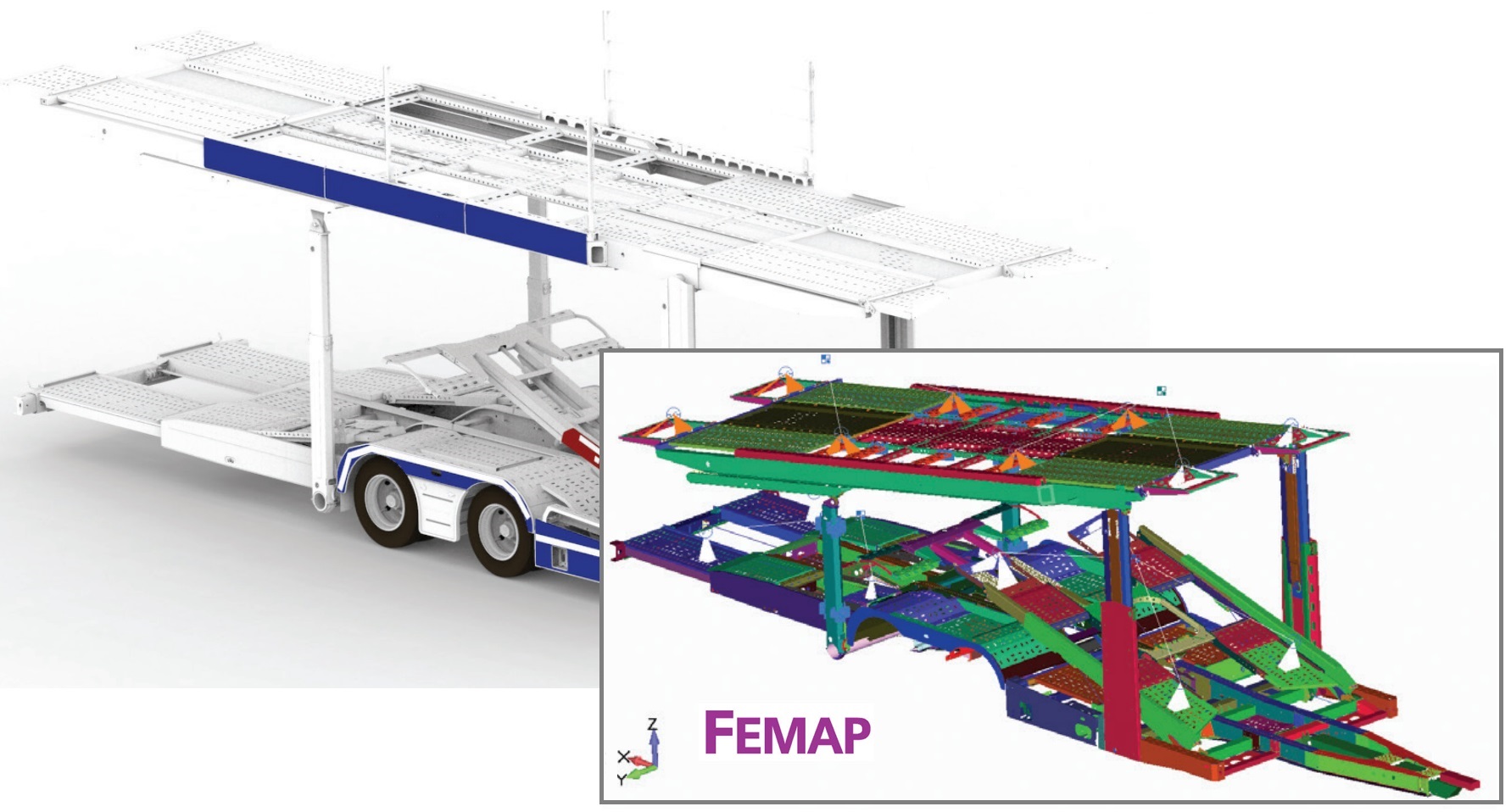
Рис. 1. Геометрическая (САПР Solid Edge) и конечно-элементная (Simcenter Femap) модели автовоза
Примеры и анализ расчетных конечно-элементных моделей в автомобилестроении
На рис. 1 изображены геометрическая (САПР Solid Edge) и конечно-элементная (КЭ) модели автовоза. КЭ-модель подготовлена в Simcenter Femap с NX Nastran от Siemens Digital Industries Software. Производитель данного автовоза – австрийская компания Kässbohrer Transport Technik GmbH.
КЭ-модель состоит преимущественно из поверхностных конечных элементов, что позволило значительно снизить размерность модели по сравнению с решением на основе объемных конечных элементов. Нагрузки от транспортируемого автомобиля передаются через жесткие RBE конечные элементы, соединяющие условные сосредоточенные массы и «пятна» контактов шин. Размерность КЭ-модели определяется количеством узлов сетки, которое зависит от количества и типа конечных элементов.
Величина модели при использовании МКЭ непосредственным образом не определяет количество конечных элементов – большее значение имеет детализация модели. Например, глобальная (без проработки узлов конструкции) конечно-элементная модель стометрового моста может состоять из меньшего числа конечных элементов, чем модель небольшого кронштейна сложной геометрии.
КЭ-модель автовоза состоит преимущественно из поверхностных КЭ и позволяет определить напряженно-деформированное состояние не только в несущих профилях (балках), но и в узлах металлоконструкции, соединительных усиливающих пластинах, перфорированных листах покрытия.
На рис. 2 изображена КЭ-модель грузовой эстакады, состоящая из балочных конечных элементов. Модель достаточно проста, но при этом в ней учтены основные конструктивные элементы, определяющие жесткость конструкции. Такое решение позволяет проверить на прочность, устойчивость выбранные балки и быстро произвести оптимизацию модели.
Подготовить балочную модель можно за несколько часов, расчет на современных вычислительных машинах, как правило, занимает не больше нескольких минут – в этом основное преимущество балочных моделей. Однако в связи с низкой детализацией (узлы не построены) необходим отдельный расчет сильно нагруженных узлов конструкции. Для этого требуется извлечь полученные в результате расчета усилия в узлах, реакции в местах закрепления. Как подготовить КЭ-модель грузовой эстакады в Simcenter Femap с NX Nastran и произвести расчет на прочность, можно посмотреть в записи моего вебинара «Экспресс-оценка металлокаркаса грузовой эстакады в Femap с NX Nastran».

Рис. 2. Конечно-элементная модель грузовой эстакады
Справедлива общая закономерность: одномерные конечные элементы проще и экономнее (с точки зрения машинных мощностей, так как число узлов намного меньше), чем поверхностные КЭ; поверхностные КЭ проще и экономнее, чем объемные КЭ. Решать задачи механики изделий какой угодно геометрической формы позволяют только объемные КЭ. При этом важно понимать специфику работы КЭ в конкретном изделии и хорошо представлять, какие локальные погрешности возникают в связи с применением того или иного подхода.
На рис. 3 показаны две КЭ-модели одного и того же изделия. Модель, выполненная из объемных КЭ (Solid), состоит из 53 240 узлов (Nodes); модель из поверхностных КЭ (Shell) включает 11 069 узлов.

Рис. 3. КЭ-модели изделия, состоящие из объемных (Solid) и поверхностных (Shell) конечных элементов
Сложные задачи вынуждают использовать все виды конечных элементов, причем наиболее рациональным оказывается сочетание КЭ разных типов. На рис. 4 изображены части конечно-элементной модели легкового автомобиля от компании Axon Automotive.

Рис. 4. Части конечно-элементной модели автомобиля от компании Axon Automotive
Силовые балки (Vehicle Beam) автомобиля смоделированы балочными КЭ; аппаратура, оборудование, кронштейны (Vehicle Equipment) – балочными, жесткими и объемными КЭ; упругие элементы, амортизаторы (Springs) – КЭ типа Springs; связевые элементы автомобиля (Vehicle Joints) – жесткими конечными элементами типа RBE, а панели, листовые детали (Vehicle Panels) – поверхностными КЭ. Создание такой КЭ-модели требует от инженеров-расчетчиков высокого уровня профессионализма и фундаментальных знаний в области механики сплошной среды. Подробнее о различных подходах к созданию расчетных КЭ-моделей можно прочитать в статье «Оптимальная расчетная конечно-элементная модель. Способы соединения частей КЭ-модели».
Некоторые ответственные узлы и детали требуют особо тщательного изучения, анализа. Такой анализ можно провести с помощью конечно-элементных моделей высокой детализации. Примером подобного узла является узел подвески внедорожника Trophy Truck от Honda Off-Road Racing. Расчет узла в Simcenter Femap с NX Nastran выполнил Дэвид Хааг из Haag Enterprises.
Внедорожник Trophy Truck (рис. 5) — это транспортное средство, используемое в гонках по бездорожью. Большинство компонентов подвески данной машины составляют сварные детали из листового металла, изготовленные мастерами отрасли. При правильном проектировании такой подход позволяет получить жесткую и легкую конструкцию. Ниже мы разберем, какой методикой и какими инструментами, приемами пользовались специалисты Haag Enterprises при расчете узла подвески Trophy Truck.

Рис. 5. Внедорожник Trophy Truck
Рекомендация №1. Заполнение зазоров между серединными поверхностями
Компания Hall Designs – один из производителей, которые используют подход, представленный выше. Как видно на рис. 6, узел задней подвески состоит из 19 частей, составляющих сварную конструкцию рычага подвески. 17 из них представляют собой детали из тонкого листового металла, обрабатываемого лазером с последующей формовкой. Части детали соединяются посредством сварки вольфрамовым электродом.

Рис. 6. Сварной элемент рычага подвески состоит из 19 деталей (семнадцать из них из листового металла)
Для анализа сварного соединения рычага задней подвески с использованием конечно-элементного анализа геометрические модели тонкостенных деталей рационально преобразовать в серединные поверхности – с целью создания сетки поверхностных конечных элементов. Но серединные поверхности имеют нулевую толщину, и, как следствие, возникают зазоры между соседними компонентами (рис. 7).

Рис. 7. Тонкие пластины преобразованы в серединные поверхности, возникают зазоры между Т-образными соединениями и сопряженными пластинами детали
Инженеру-прочнисту требуется устранить эти зазоры для правильной передачи нагрузок между соседними частями детали. На рис. 8 показана общая стратегия устранения зазоров в Т-образных соединениях путем удлинения краев поверхности до пересечения с соседними поверхностями.
С использованием инструментов Meshing Toolbox → Geometry Editing → Extend (Создание сетки → Редактирование геометрии → команда Вытянуть) красные кривые на серой части выделяются и удлиняются до сплошного синего листа. Одновременно отображается кривая, на которой при создании сетки будут располагаться общие узлы. Сами по себе эти шаги не представляют большой сложности, но для моделей сборок с большим количеством компонентов задача становится весьма трудоемкой: необходимо, во-первых, находить Т-образные соединения, а, во-вторых, отслеживать, какие из них были исправлены.

Рис. 8. Применение инструментов Создание сетки → Редактирование геометрии → команда Вытянуть
Рекомендация № 2. Быстрый способ определения местоположения и доработки Т-образных соединений серединных поверхностей
Панель инструментов управления сеткой (Mesh Control Explorer) в Simcenter Femap помогает автоматизировать процесс распространения сетки конечных элементов между телами и поверхностями, у которых отсутствуют совпадающие края. Также этот инструмент можно использовать для поиска Т-образных соединений между поверхностями.
На рис. 9 показаны справочные номера команд, используемых в процессе определения Т-образных соединений тел. Ниже мы проанализируем панель инструментов и обсудим некоторые примеры рабочих процессов.
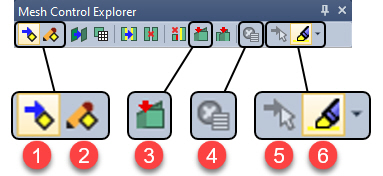
Рис. 9. Панель инструментов управления сеткой (Mesh Control Explorer) с увеличенными кнопками команд и ссылочными номерами
Описание команд
1. Включение/выключение панели инструментов (Toggle Toolbar On/Off).
При создании сетки модели эту панель инструментов можно в любое время включать и отключать. При отключенной панели параметры и настройки игнорируются во время операций с сеткой.
2. Параметры распространения размеров сетки (Mesh Sizing Propagation Options).
Ограниченный выбор (Limit Selection) – команда определяет, какие твердые тела/поверхности учитываются при обновлении размеров сетки. Если используется только выбранное твердое тело, нажмите кнопку Выбрать твердые тела, чтобы выбрать твердые тела, листовые твердые тела и сложные тела с помощью диалогового окна Выбор стандартного объекта.
На твердых телах (On Solids), если включены подчиненные (Slaved) и преображенные (Mapped) поверхности, подчиненные поверхности с преображенными сетками учитываются при определении того, какие ребра обновлять. В противном случае эти поверхности не учитываются.
Ребра для сопряжения (Edges to Pair). При установке данного параметра будут автоматически найдены соседние ребра «несшитых» геометрических объектов (то есть отдельных поверхностей, твердых тел и/или частей «незамкнутого объема»), а размеры сетки будут сопоставлены по нескольким совпадающим краям.
Допуск сопряжения ребер (Edge Pairing Tolerance). Это допуск, используемый для автоматического «сопряжения» совпадающих ребер. Автоматический использует допуск слияния узлов по умолчанию, а Указанный использует значение, заданное пользователем.

Рис. 10. Параметры размеров сетки, используемые для модели узла подвески
При создании модели узла подвески внедорожника были использованы только настройки «для выбранных твердых тел». Выбраны компоненты с зазорами между Т-образными соединениями. «Подчиненные» или «преображенные» поверхности не определялись, так что в нашем примере эти флажки-настройки не будут иметь никакого эффекта. Листовой металл в исследуемой сварной детали имеет толщину 0,090 дюйма, поэтому между кромками должен быть зазор такого же размера, 0,090 дюйма (половина толщины материала × 2). В модели узла подвески был установлен допуск сопряжения кромок на 0,125 дюйма, чтобы обеспечить захват всех интересующих кромок.
3. Отображение ребер, прилегающих к поверхностям с «отпечатанным» краем (Show Edges that are Adjacent to Surfaces with no Imprinted Edge).
Эта команда визуально выделит все ребра, прилегающие к грани поверхности и попадающие в пределы указанного допуска сопряжения ребер (см. рис. 7). Но сначала необходимо включить подсветку (№ 6 на рис. 9).
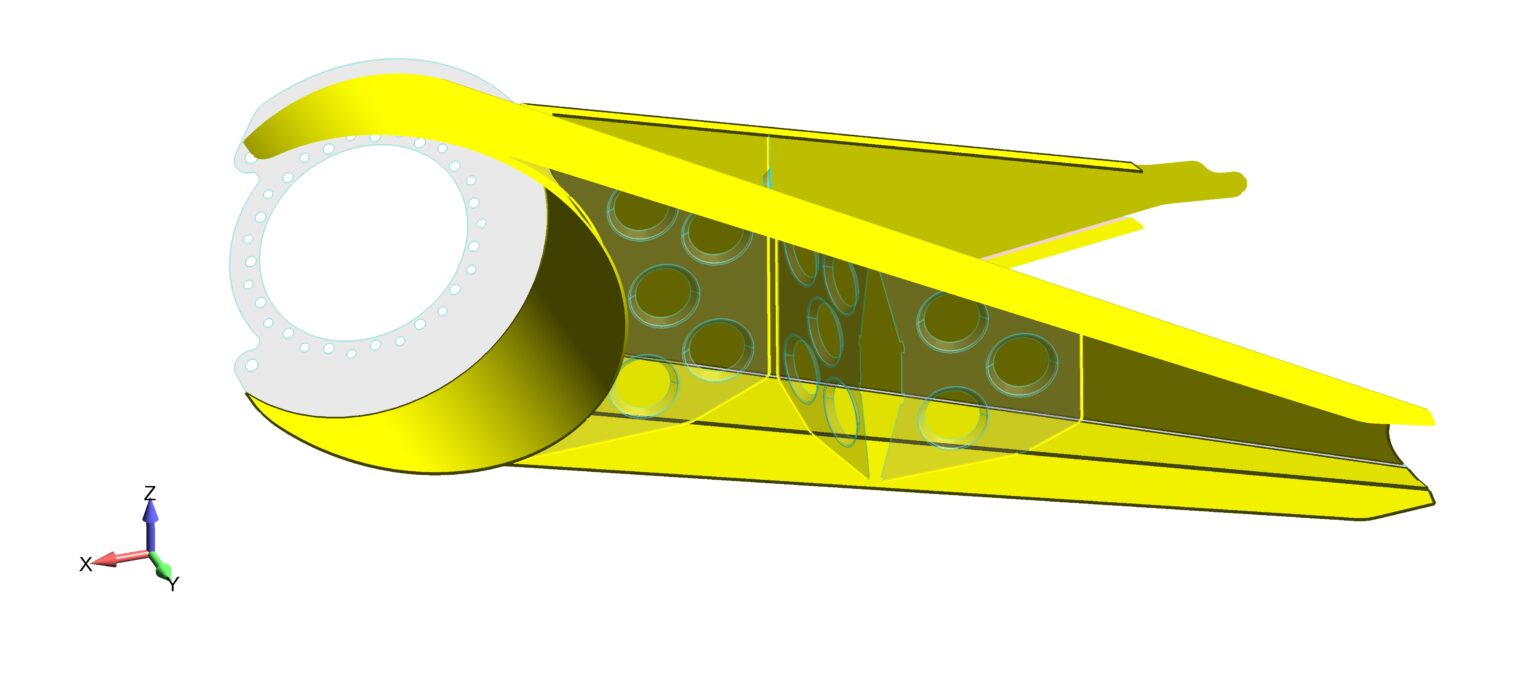
Рис. 11. Команда Отобразить ребра, прилегающие к поверхностям с «не отпечатанным» краем, выполняемая на основе выбранных твердых тел. Парные края, соответствующие критериям, выделяются и отображаются в виде списка на панели инструментов управления сеткой (Mesh Control Explorer)
У пользователя есть возможность детализировать и назначить действия интересующим парам тел (Imprint Edges). На рис. 12 видно, что под панелью инструментов отображается список – каждую линию можно выбрать из списка, где отображены парные кривые в графической области. Таким образом пользователь получает мгновенную визуальную обратную связь. Список действий и опций доступен при щелчке правой кнопкой мыши в области списка и функционирует следующим образом:
• Отпечаток ребер (Imprint Edges) – действие применяется только к выбранной паре, «подсвечивает» кривую/ребро на соседнюю поверхность (см. рис. 12);

Рис. 12. Список действий и параметров, доступных по щелчку правой кнопкой мыши в области списка
Отпечаток ребер – Все (Imprint Edges – All) – «подсвечивает» кривые/ребра, найденные во всем списке, на соответствующие смежные поверхности;
Вытянуть отпечатки (Extend Imprints) – опция позволяет отпечатанному краю вытянуться до следующей кривой на его пути (рис. 13).
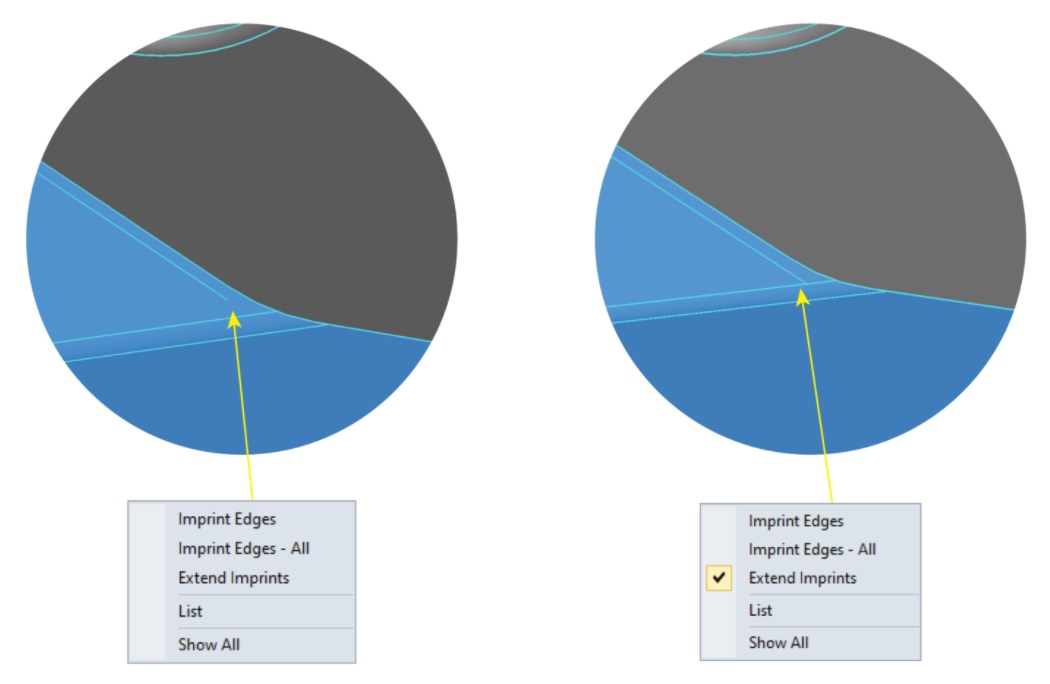
Рис. 13. Разница действий при установленном и снятом флажке Вытянуть отпечатки (Extend Imprints)
4. Очистить список контроля сетки (Clear Mesh Control Explorer List).
Команда очищает список пар.
5. Выберите объект для размещения в списке (Select Entity to Locate in List).
Параметр Показать все удобен для общего обзора, но когда пришло время поработать над определенным сочетанием, нам понадобится быстрый способ выбора из списка, особенно если список длинный. Используя команду №5 (см. рис. 9), мы можем выбрать поверхность в графической области – и пара будет выделена в списке, как показано на рис. 14.

Рис. 14. При выборе поверхности в графической области пара будет выделена в списке
6. Показывать при выборе (Show When Selected) – рис. 15.
Содержит несколько параметров для отображения объектов, выделенных в данный момент в окне управления сеткой (Mesh Control Explorer) главного графического окна. Какие будут показаны кривые и поверхности, типы отображаемых объектов – зависит от того, какой инструмент использовался для заполнения списка в окне управления сеткой.

Рис. 15. Доступ к параметрам Показывать при выборе можно получить, щелкнув по стрелке, расположенной справа от кнопки.
Пример рабочего процесса и основные выводы
То, как мы будем моделировать зазор Т-образного перехода, зависит от конкретной задачи. В примере узла подвески автор использовал Mesh Control Explorer для визуальной проверки, чтобы убедиться, что все зазоры Т-образных соединений закрыты с помощью команды Extend в Meshing Toolbox, которая по умолчанию будет дорабатывать края. После удлинения всех поверхностей для устранения зазоров Т-образного соединения можно (используя команду Показать края) проверить края, которые примыкают к поверхностям без отпечатанных краев (№ 3 на рис. 9). Если результат нулевой, то каждое из пересечений находится рядом и сетка имеет общие узлы.
Одним из ключевых моментов при использовании окна управления сеткой Mesh Control Explorer является то, что перед построением сетки нам больше не нужно создавать очень сложные тела (Non-Manifold). Такой подход имеет важные преимущества:
- если происходят изменения, нет необходимости восстанавливать существовавшую или добавлять новую геометрию, а затем снова использовать функцию non-manifold;
- если области контакта были определены, то при восстановлении геометрии non-manifold выбранные грани иногда теряют ассоциативность, а это требует дополнительной работы для исправления.
В рамках этой статьи мы рассмотрели несколько примеров глобальных расчетных конечно-элементных моделей изделий автомобилестроения (автотранспортера, грузовой эстакады, легкового автомобиля), модель узла подвески трюкового внедорожника, проанализировали концептуальные подходы, использованные при их создании. На примере узла подвески проанализировали одну из сложностей, с которыми при создании поверхностной конечно-элементной модели сталкивается инженер-прочнист, получая в качестве исходных данных объемную геометрическую модель: зазоры между сгенерированными серединными поверхностями. Зазоры можно быстро обнаружить и устранить инструментами панели управления сеткой препроцессора Simcenter Femap.
Мы разбирали примеры из области автомобилестроения, однако МКЭ эффективно и широко используется и в других отраслях. Таким образом, метод конечных элементов и расчетные комплексы, в основу которых этот метод положен, являются сегодня одними из самых эффективных инструментов для решения задач механики, расчета и оптимизации конструкций.
Источник: habr.com