Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.
В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.
Формулы сокращенного умножения. Таблица
Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.
Формулы сокращенного умножения
- формула квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
- формула квадрата разности: a — b 2 = a 2 — 2 a b + b 2
- формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
- формула куба разности: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
- формула разности квадратов: a 2 — b 2 = a — b a + b
- формула суммы кубов: a 3 + b 3 = a + b a 2 — a b + b 2
- формула разности кубов: a 3 — b 3 = a — b a 2 + a b + b 2
Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.
ЭТАПЫ СТРОИТЕЛЬСТВА И РЕМОНТА ДОМА. КАКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ?

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.
Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.
Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.
Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.
При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Дополнительные формулы сокращенного умножения
Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.
Во-первых, рассмотрим формулу бинома Ньютона.
a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . + C n n — 1 · a · b n — 1 + C n n · b n
Здесь C n k — биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике паскаля. Биномиальные коэффициенты вычисляются по формуле:
C n k = n ! k ! · ( n — k ) ! = n ( n — 1 ) ( n — 2 ) . . ( n — ( k — 1 ) ) k !
Как видим, ФСУ для квадрата и куба разности и суммы — это частный случай формулы бинома Ньютона при n=2 и n=3соответственно.
Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.
a 1 + a 2 + . . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n — 1 a n
Как читать эту формулу? Квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Еще одна формула, которая может пригодится — формула формула разности n-ых степеней двух слагаемых.
a n — b n = a — b a n — 1 + a n — 2 b + a n — 3 b 2 + . . + a 2 b n — 2 + b n — 1
Эту формулу обычно разделяют на две формулы — соответственно для четных и нечетных степеней.
Для четных показателей 2m:
a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 + . . + b 2 m — 2
Для нечетных показателей 2m+1:
a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 + . . + b 2 m
Формулы разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы при n = 2 и n = 3 соответственно. Для разности кубов b также заменяется на — b .
Как читать формулы сокращенного умножения?
Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.
a + b 2 = a 2 + 2 a b + b 2 .
Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.
Все остальные формулы читаются аналогично. Для квадрата разности a — b 2 = a 2 — 2 a b + b 2 запишем:
квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.
Прочитаем формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.
Переходим к чтению формулы для разности кубов a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3 . Куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.
Пятая формула a 2 — b 2 = a — b a + b (разность квадратов) читается так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.
Выражения типа a 2 + a b + b 2 и a 2 — a b + b 2 для удобства называют соответственно неполным квадратом суммы и неполным квадратом разности.
С учетом этого, формулы суммы и разности кубов прочитаются так:
Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.
Доказательство ФСУ
Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.
Для примера рассмотрим формулу квадрата разности.
a — b 2 = a 2 — 2 a b + b 2 .
Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.
a — b 2 = a — b a — b .
a — b a — b = a 2 — a b — b a + b 2 = a 2 — 2 a b + b 2 .
Формула доказана. Остальные ФСУ доказываются аналогично.
Примеры применения ФСУ
Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.
Упростим выражение 9 y — ( 1 + 3 y ) 2 .
Применим формулу суммы квадратов и получим:
9 y — ( 1 + 3 y ) 2 = 9 y — ( 1 + 6 y + 9 y 2 ) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2
Сократим дробь 8 x 3 — z 6 4 x 2 — z 4 .
Замечаем, что выражение в числителе — разность кубов, а в знаменателе — разность квадратов.
8 x 3 — z 6 4 x 2 — z 4 = 2 x — z ( 4 x 2 + 2 x z + z 4 ) 2 x — z 2 x + z .
Сокращаем и получаем:
8 x 3 — z 6 4 x 2 — z 4 = ( 4 x 2 + 2 x z + z 4 ) 2 x + z
Также ФСУ помогают вычислять значения выражений. Главное — уметь заметить, где применить формулу. Покажем это на примере.
Возведем в квадрат число 79 . Вместо громоздких вычислений, запишем:
79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .
Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.
Еще один важный момент — выделение квадрата двучлена. Выражение 4 x 2 + 4 x — 3 можно преобразовать в вид 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4 . Такие преобразования широко используются в интегрировании.
Источник: zaochnik.com
Общие правила в строительстве

Задания и ответы школьного этапа 2022 всероссийской олимпиады школьников ВСОШ по Химии 7−11 классов на платформе «Сириус Курсы» пройдет 4-7 октября согласно графику проведения.


1. Определите, какие водные растворы изображены на рисунках.
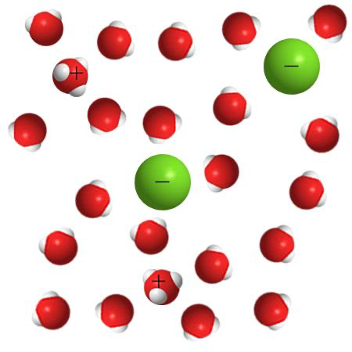
Раствор щёлочи
Раствор сильной кислоты
Раствор слабой кислоты
Раствор соли
Раствор неэлектролита
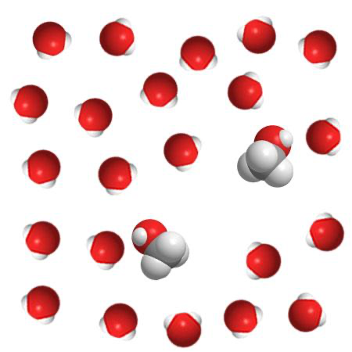
Раствор щёлочи
Раствор сильной кислоты
Раствор слабой кислоты
Раствор соли
Раствор неэлектролита
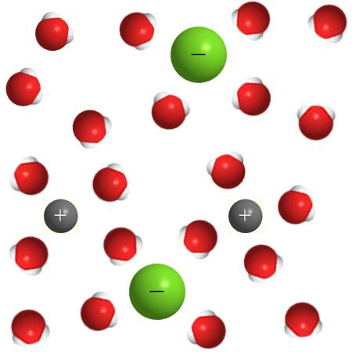
Раствор щёлочи
Раствор сильной кислоты
Раствор слабой кислоты
Раствор соли
Раствор неэлектролита
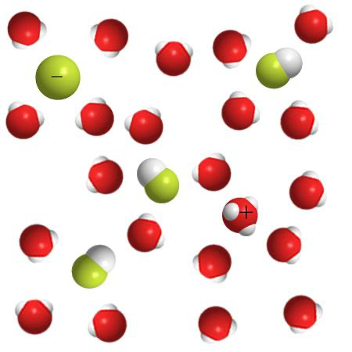
Раствор щёлочи
Раствор сильной кислоты
Раствор слабой кислоты
Раствор соли
Раствор неэлектролита
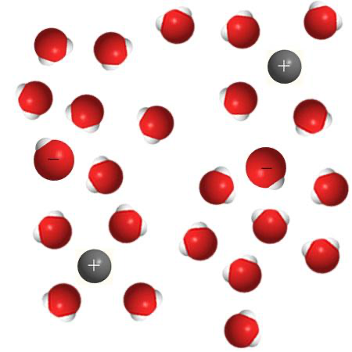
Раствор щёлочи
Раствор сильной кислоты
Раствор слабой кислоты
Раствор соли
Раствор неэлектролита
2. В воде растворили 0.2 моль вещества. В полученном растворе общее количество положительных и отрицательных ионов превышает 0.55 моль. Какое вещество могло быть растворено? Выберите все верные ответы:
3. Решите химический кроссворд. Ответами являются химические формулы веществ. Каждую букву и цифру формулы вещества необходимо записать в отдельную строку справа.
Ядовитый газ, образующийся при неполном сгорании топлива.
Пищевая сода.
Самый лёгкий газ среди сложных веществ.
Ион, образующися при диссоциации азотной кислоты.
Трёхосновная кислота.
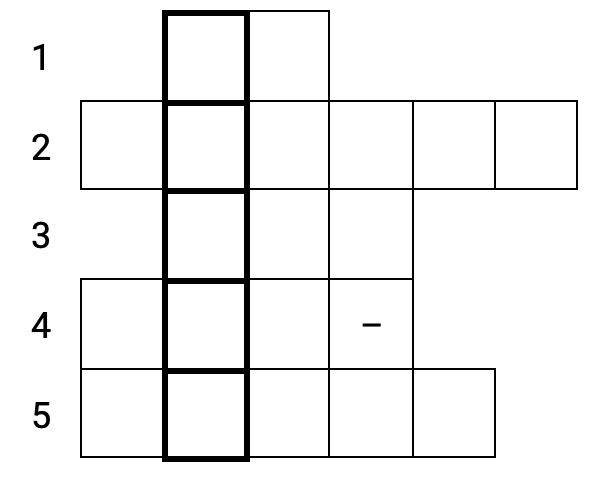
В выделенной области у вас должна получиться формула широко используемого в искусстве и в строительстве минерала. Запишите название минерала, состоящее из 6 букв, в именительном падеже:

4.Установите соответствие между описанием реакции и реагирующими веществами.
При смешении двух бесцветных растворов выпадает жёлтый осадок
В водном растворе не протекает
Является окислительно-восстановительной
KI и Pb(NO3)2
FeCl2 и Na2S
KI и AgNO3
FeCl3 и H2S
HCl и AgNO3
NaNO3 и BaCl2
5. Смеси гелия с кислородом под общим названием «Гелиокс» используют для глубоководных погружений и лечения заболеваний дыхательных путей. Гелиокс 60/40 содержит 60 % гелия по объёму. Во сколько раз он тяжелее чистого гелия (при одинаковых условиях)? Ответ округлите до десятых.
6. Неизвестное вещество X состоит из ионов, имеющих такую же электронную конфигурацию, как и атом неона. Оно представляет собой белый порошок, реагирующий с соляной кислотой с образованием бесцветного раствора. При действии на полученный раствор гидроксидом натрия выпадает белый осадок, нерастворимый в избытке щёлочи.

Сколько всего электронов находится на p‑орбиталях в атоме неона?
Запишите химическую формулу вещества X.
При спекании вещества X с оксидом алюминия образуется бесцветное вещество, встречающееся в природе в виде минерала Y. Запишите формулу этого минерала, если известно, что X реагирует с оксидом алюминия в мольном соотношении 1:1.
7. В ёмкости находится бесцветный раствор. При выливании на керамическую плитку спустя некоторое время он самопроизвольно загорается. Горение сопровождается выделением белого дыма и образованием синего пламени. Твёрдого нелетучего остатка от сгорания не остается.
Продукты сгорания при пропускании их над безводным сульфатом меди (II) не вызывают изменения его окраски.
Выберите возможный растворитель:
Этиловый спирт C2H5OH
Вода
Сероуглерод CS2
Гексан C6H14
Выберите возможное растворённое вещество:
Cера S
Белый фосфор P4
Хлорид натрия NaCl
Метан CH4
Белый дым при остывании оседает в виде белого порошка. Найдите массу этого порошка, образующегося при сгорании 124 г 10 %‑го исследуемого раствора. Ответ выразите в граммах, округлите до десятых.

8.В пробирках выданы растворы следующих солей натрия: хлорид, карбонат, силикат, сульфид и фосфат. Из каждой пробирки отобрали пробы растворов объёмом 1 мл, к которым добавили соляную кислоту. В таблице представлены результаты эксперимента:
Выделился газ без цвета и без запаха
Карбонат натрия
Фосфат натрия
Хлорид натрия
Силикат натрия
Сульфид натрия
Выпал бесцветный студнеобразный осадокКарбонат натрия
Фосфат натрия
Хлорид натрия
Силикат натрия
Выделился бесцветный газ с неприятным запахомКарбонат натрия
Фосфат натрия
Хлорид натрия
Силикат натрия
Без изменений; после добавления раствора CaCl2 также без измененийКарбонат натрия
Фосфат натрия
Хлорид натрия
Силикат натрия
Без изменений; после добавления раствора CaCl2 выпал белый осадокКарбонат натрия
Фосфат натрия
Хлорид натрия
Силикат натрия
Каждому опыту поставьте в соответствие исследуемое вещество.

9. Для разрыва химической связи в молекулах H2 и Cl2 требуется 218 и 120 единиц энергии соответственно, а при образовании одной молекулы HCl из атомов H и Cl выделяется 215 единиц энергии. Сколько единиц энергии выделяется при образовании 2 молекул HCl из молекул H2 и Cl2? Ответ округлите до целых.
10. На химическом производстве используют смесь двух газов, плотность которой в 2 раза меньше плотности смеси равных объёмов азота и кислорода (при одинаковых условиях). При сгорании этой смеси образуются газ, вызывающий помутнение известковой воды, и бесцветная жидкость, которая при добавлении к безводному сульфату меди (II) придаёт веществу синюю окраску.
Запишите в любом порядке формулы газов, входящих в состав искомой смеси.
Сколько молекул более тяжелого газа приходится на одну молекулу более лёгкого газа в смеси?
Число
Чему равна относительная плотность смеси по водороду? Ответ округлите до десятых.
11. В лаборатории провели три опыта.Опыт 1. В пробирку (см. рисунок) поместили вещество А жёлто‑оранжевого цвета и нагрели. Из пробирки выделялся газ Б, не имеющий ни цвета, ни запаха, поддерживающий горение. В пробирке остались капельки металла В серебристого цвета. Металл В не реагирует ни с соляной кислотой, ни с разбавленной серной кислотой.
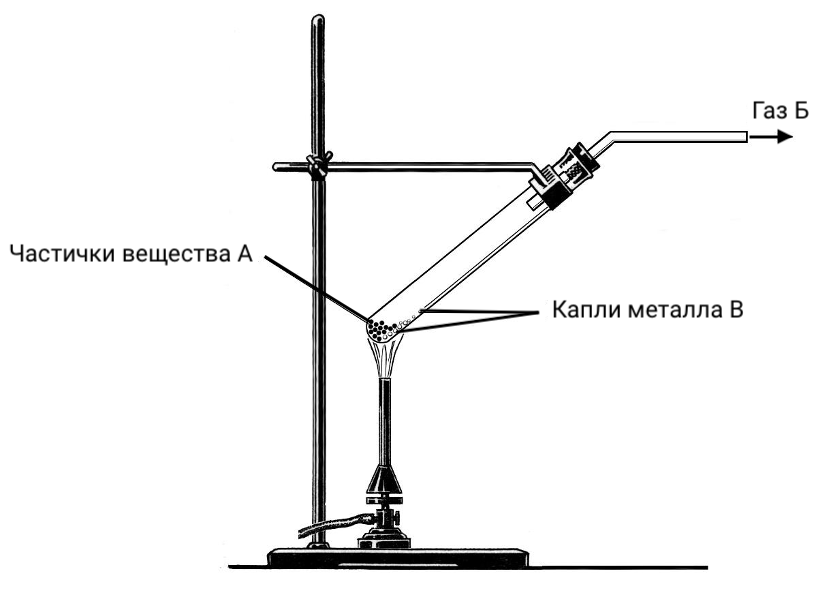
Опыт 2. Вещество А растворили в соляной кислоте и получили бесцветный раствор вещества Г. Часть раствора Г перенесли в пробирку и пропустили через него сероводород, при этом наблюдали выпадение в осадок вещества Д чёрного цвета. Вещество Д встречается в природе. Кристаллы природного Д могут иметь красную окраску.
Опыт 3. Во вторую часть раствора Г внесли хорошо зачищенную медную пластинку. На поверхности пластинки выделился блестящий слой металла В.
Известно, что Б и В — простые вещества. Вещества А, Г и Д состоят из двух элементов. Вещества А, Г и Д содержат атомы одного и того же химического элемента со степенью окисления +2.
Определите вещества А–Д и запишите их формулы.
12. Круглодонную колбу объёмом 1.000 л закрыли пробкой с газоотводной трубкой и заполнили газом X при н.у. Масса газа в колбе составила 5.714 г. Затем газоотводную трубку опустили в кристаллизатор с водой (на рисунке показан цифрой 1), в которую был добавлен фиолетовый лакмус. Открыли кран (2), и вода по трубке стала подниматься вверх, внутри колбы «забил фонтан».
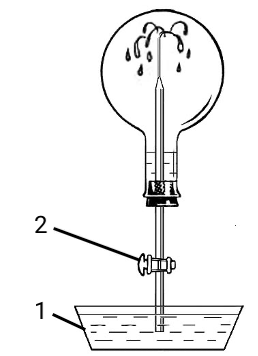
Лакмус в растворе внутри колбы принял красную окраску. Для того, чтобы лакмус снова принял фиолетовую окраску, потребовалось добавить в раствор 2.500 г гидроксида калия.
Определите газ X и запишите его формулу.
Источник: pndexam.ru
Золотая осень без дождей не обойдется. Атмосферный фронт приходит в Петербург

Как рассказал 11 октября в своем телеграм-канале ведущий специалист центра «ФОБОС» Михаил Леус, сегодня город на Неве окажется на пути холодного атмосферного фронта, который скроет солнце за облаками и усилит ветер, а во второй половине дня ожидаются небольшие дожди.
Температура воздуха составит +11…+13 градусов. Ветер юго-западный 4–9 м/с, порывистый. Атмосферное давление — 758 мм рт. ст., что ниже нормы.
В ночь на среду похолодает до +5. +7 градусов, а в пригородах и вовсе до +3. Днем потеплеет до +9. +11 градусов и пройдут небольшие дожди, обещают синоптики УГМС.

Больше интересных новостей в нашем официальном телеграм-канале «Фонтанка SPB online». Подписывайтесь, чтобы первыми узнавать о важном.
По теме
11 октября 2022, 11:31
08 октября 2022, 11:24
21 апреля 2022, 08:06
10 сентября 2022, 10:40
27 августа 2022, 10:17
Пока нет ни одного комментария.
Добавьте комментарий первым!
ПРИСОЕДИНИТЬСЯ
Самые яркие фото и видео дня — в наших группах в социальных сетях
Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter
Отправьте свою новость в редакцию, расскажите о проблеме или подкиньте тему для публикации. Сюда же загружайте ваше видео и фото.
Написать в редакцию
Новости компаний



О компании
Рассылка новостей
Рубрики
Сообщить новость
Проекты
О компании
Мобильное приложение
Мы в соцсетях
Контактные данные для Роскомнадзора и государственных органов
«Фонтанка» — петербургская интернет-газета, где можно найти не только новости Петербурга, но и последние новости дня, и все важное и интересное, что происходит в России и в мире. Здесь вы отыщете наиболее значимые происшествия, новости Санкт-Петербурга, последние новости бизнеса, а также события в обществе, культуре, искусстве. Политика и власть, бизнес и недвижимость, дороги и автомобили, финансы и работа, город и развлечения — вот только некоторые из тем, которые освещает ведущее петербургское сетевое общественно-политическое издание. Санкт-Петербург читает «Фонтанку»! Наша аудитория — лидеры бизнеса и политики, чиновники, десятки тысяч горожан.
Источник: www.fontanka.ru