В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.
В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.
Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.
Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.
Поперечные силы и изгибающие моменты
При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (Mизг).

Как строить сечения

Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.
Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.
Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!
Обозначения поперечных сил и изгибающих моментов
Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.
Например, если выбрать следующие обозначения для координатных осей:

То, поперечная сила, будет обозначаться, как Qy (параллельна оси y), а изгибающий момент, как Mx (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Qy, Mz или Qz, Mx. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – Mизг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.
#Физика. Электричество. Поперечное сечение проводника fiz1.ru
Расчётная схема балки
Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.
К примеру, балка может иметь прямоугольное поперечное сечение:

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.
Правила знаков для поперечных сил и изгибающих моментов
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).
Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и Мизг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).
Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.
Правило знаков для поперечных сил
Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:

Правило знаков для изгибающих моментов
Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.
На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;

• нижние волокна, то нужно учесть его с «плюсом».

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.
Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:

Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:


Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:

Как построить эпюры поперечных сил и изгибающих моментов ?
В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.
Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике
Построение эпюр для консольной балки
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Будем рассчитывать балку справа налево.
Рассмотрим первый участок
Обозначим некоторое сечение 1-1 на расстоянии x1, от свободного торца балки, при этом x1 будет находиться в диапазоне: 0 ≤ x1 ≤ 4м.

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.
Поперечные силы на первом участке
Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:

Как видишь, поперечная сила будет постоянна на первом участке:

Уже можем отразить это на эпюре поперечных сил:

Изгибающие моменты на первом участке
Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:

Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Расчёт второго участка
Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x2 от начала участка (0 ≤ x2 ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке
Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:

Теперь можем показать окончательную эпюру поперечных сил:

Изгибающие моменты на втором участке
Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:

Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Проверка построенных эпюр
Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.
Определение реакций в жёсткой заделке


Расчёт эпюр поперечных сил и изгибающих моментов
Рассчитываем все участки теперь слева направо:


Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.
Эпюра моментов со стороны растянутых или сжатых волокон
По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.
Причем сама эпюра была построенна со стороны растянутых волокон:

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.
Учёт распределённой нагрузки
Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Определение поперечной силы и изгибающего момента в сечении A
Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.
После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Тогда поперечная сила QA будет равна:

Изгибающий момент Mизг, A будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов
Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Уравнение для поперечных сил будет следующее:

Рассчитаем значения на эпюре поперечных сил:


Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:


На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.
Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

Построение эпюр для двухопорной балки
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

Определим реакции опор:


Рассчитываем первый участок:

Строим эпюры на первом участке:

Определение экстремума на эпюре моментов
Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.
Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:

Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Расчет эпюр на остальных участках
Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:



Оценка правильности построенных эпюр поперечных сил и изгибающих моментов
И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.
Вот несколько признаков, правильно построенных эпюр:
- На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
- На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
- Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
- Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.
1 комментарий
Опубликовал новую статью по построению эпюр для балок. Позднее планирую добавить в статью примеры по построению эпюр для плоских рам. Если будут какие-нибудь вопросы по уроку, можешь спросить здесь.
Источник: ssopromat.ru
Расчет площади поперечного сечения сварного шва
Перед тем как раскрыть основное понятие, нужно расшифровать значение термина и понять, чем провод отличается от кабеля. Провод является проводником, который используется, чтобы соединить несколько участков электрической цепи. Может иметь одну или много токовых проводящих жильных элементов. Они в свою очередь могут быть голыми, изолированными, одножильными и многожильными.

Площадь среза проводника
Первые используются в воздушных линиях электрических передач. Вторые применяются в электрических устройствах, щитках или шкафах. В быту они находятся внутри электрической проводки.
К сведению! Изолированные и одножильные проводники используются везде, а многожильные применяются там, где нужны изгибы с малым радиусом.

Что собой представляет поперечное сечение
Поперечным сечением называется фигура, которая образуется от проводникового рассечения плоскостью направления. Площадь, которая получена при перпендикулярном разрезе любого вида провода, указывается в квадратных миллиметрах. Это важный параметр для расчета электрической сети.
Шар и сфера, их сечения
Напомним, что шаром
называется тело, состоящее из всех точек пространства, находящихся на расстоянии не большем заданного от некоторой данной точки. Эта точка –
центр
шара, а заданное расстояние –
радиус
шара.
Шар так же, как цилиндр и конус, является телом вращения. Он получается в результате вращения полукруга вокруг его диаметра.
Поверхность, образуемая при этом вращении полуокружности, называется сферой
. Можно сказать, что сфера – это как бы оболочка, или граница, шара. Как окружность есть граница круга, так и сфера – это граница шара.
Назовём элементы сферы и шара.
сферы – это отрезок, соединяющий центр сферы и любую её точку.
сферы – отрезок, соединяющий две точки сферы.
сферы – хорда сферы, проходящая через её центр.
Радиус, хорда, диаметр шара – это радиус, хорда, диаметр его сферы.
Любое сечение шара плоскостью есть круг. Центром этого круга является основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Плоскость, которая проходит через центр шара, называется диаметральной плоскостью
. Сечение ею шара –
большим кругом
, а сечение сферы –
большой окружностью
.
Любая диаметральная плоскость шара является его плоскостью симметрии
. Центр шара является его
центром симметрии
.
Плоскость, проходящая через точку А
сферы и перпендикулярно радиусу, проведённому в эту точку, называется
касательной плоскостью
. Точка
А
называется
точкой касания
.
Свойство касательной плоскости к сфере
: радиус сферы, проведённый в точку касания, перпендикулярен касательной плоскости.
Признак касательной плоскости к сфере
: плоскость, перпендикулярная радиусу сферы в конечной его точке на сфере, является касательной к сфере.
Касательная плоскость пересекается с шаром в единственной точке – в точке касания.
Касательной прямой
к сфере (шару) называется прямая, имеющая со сферой единственную общую точку.
Отрезки касательных к сфере, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр сферы.
Линией пересечения двух сфер является окружность.
Площадь сферы
Шаровым сегментом
называется часть шара, отсекаемая от него плоскостью.
Площадь боковой поверхности шарового сегмента:
.
Объём шарового сегмента:
где – радиус шара, – высота шарового сегмента.
Шаровым сектором
называется тело, которое получается из шарового сегмента и конуса, основанием которого является сечение плоскостью данного шара.
Площадь боковой поверхности шарового сектора:
Объём шарового сектора
где – радиус шара, – высота сегмента.
Шар называется вписанным в многогранник
, а многогранник –
описанным около шара
, если поверхность шара касается всех граней многогранника.
Шар называется описанным около многогранника
, а многогранник –
вписанным в шар
, если поверхность шара проходит через все вершины многогранника.
Шар называется вписанным в цилиндр
, а цилиндр –
описанным около шара
, если поверхность шара касается оснований цилиндра и всех образующих.
Шар называется описанным около цилиндра
, если окружности оснований цилиндра принадлежат поверхности шара.
Шар называется вписанным в конус
(усечённый конус)
, а конус (усечённый конус) –
описанным около шара
, если поверхность шара касается основания (оснований) конуса и всех образующих.

Шар называется описанным около конуса (усечённого конуса)
, если окружность основания и вершина (окружности оснований) конуса принадлежат поверхности шара.

Если боковые грани пирамиды одинаково наклонены к плоскости основания, то в такую пирамиду можно вписать
Около пирамиды можно описать шар тогда и только тогда, когда около её основания можно описать окружность.
Если боковые рёбра пирамиды равны между собой (или одинаково наклонены к плоскости основания), то около такой пирамиды можно описать шар.
В призму можно вписать
шар тогда и только тогда, когда в перпендикулярное сечение этой призмы можно вписать окружность, а высота призмы равна диаметру окружности, вписанной в это перпендикулярное сечение.
шар около призмы можно тогда и только тогда, когда призма прямая и около её основания можно описать окружность.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. Радиус шара увеличили в раза. Во сколько раз увеличился объём шара?

Задача вторая. Объём шара равен см3. Найдите диаметр шара.

Задача третья. Шар пересечен плоскостью. Площадь сечения равна см2. Расстояние от центра шара до плоскости сечения равно см. Найдите площадь поверхности шара.

Задача четвёртая. В конус с радиусом основания, равным см, и высотой, равной см, вписан шар. Найдите отношение площади боковой поверхности конуса к площади поверхности шара.

Задача пятая. Найдите объём шарового сектора, если радиус окружности его основания равен см, а радиус шара – см.

Задача шестая. Шар с радиусом см пересечён плоскостью, находящейся на расстоянии см от центра шара. Найдите площадь сечения.

Сфера применения
Поперечное сечение на чертеже изображено в виде фигуры, которая образована делением детали плоскостью. Используется в электротехнике, электричестве, когда рассматривается проводниковая жила под прямым углом к его продольной половине. Через поделенную жилу проходят электроны.
Обратите внимание! Диаметр жилы — это не сечение. Для определения площади жилы нужно использовать специальную формулу определения круга.
Зная, какая величина разреза провода, длина и удельное сопротивление, можно узнать, какое имеет сопротивление проводник электротоку, проходящий сквозь его структуру. Если неправильно подобрать разрез проводника, это может привести к возгоранию электрической проводки в системе в результате его перегрева, оплавления.
Вам это будет интересно Особенности переходного сопротивления

Строительство — основная сфера применения проводов
Целью расчета площади поперечного сечения может быть получение нужного количества электроэнергии для нормальной работы электрических приборов, исключение переплат неиспользуемым энергоносителем, подключение мощной техники к сетевому напряжению, предотвращение возгорания участка, исключение оплавки слоя изоляции, предотвращение появления короткого замыкания в бытовой и промышленной сетях. Также это может быть получение правильной организации системы освещения.
К сведению! Нормальным сечением проводника для освещения является показатель 1,5 мм² для линии и 4-6 мм² для ввода.



Таблица диаметров и сечения проводов
Формула для расчёта диаметра достаточно проста и выдаёт стандартные значения для конкретного диаметра. Поэтому часто можно увидеть в продаже соответствующие таблицы площадей круга.
Вам это будет интересно Замеры освещенности помещения
Таблица соотношений диаметров и площадей проводов
Таким способом можно пользоваться в том случае, если под рукой оказался стандартный проводник, указанный в ГОСТ. Например — при диаметре сердечника 2.8 мм площадь его сечения составит 6 мм2.
Прочитав эту статью, любой человек сможет самостоятельно рассчитать площадь поперечного сечения провода или кабеля. Это пригодится при замене старой проводки или при монтаже новой кабельной линии. Главное условия подбора – повышенная точность, так как идеального соотношения качества, простоты установки, безопасности и оптимальной цены можно добиться только после проведения кропотливых замеров.
Чем можно делать расчеты поперечного сечения
Иногда приходится измерять поперечное сечение самостоятельно, поскольку на провод не нанесена маркировка. Это не повод, чтобы не использовать его. Сперва нужно выяснить, из какого материала была сделана жила. Есть белая алюминиевая, медная красная и латунная желтая. После этого необходимо рассчитать площадь.
Для этого следует выяснить проводниковый диаметр, убрав изоляцию. Диаметр можно измерить, используя:
- штангенциркуль, микрометр;
- карандаш и линейку.
Важно! Во втором случае результат будет приблизительным. Его использовать следует в крайних случаях. Лучше рассчитывать диаметр по формуле и штангенциркулем.
Штангенциркуль
Сделать штангенциркулем можно замер провода, который имеет любые размеры. Для этого нужно поместить его между штангенциркульными щипцами. Сделать так, чтобы они смотрены на деление шкалы. Затем подсчитать значение.

Штангенциркуль
Целые числа можно получить по верхней шкале, а десятичные — по нижней.
Карандаш + линейка
Если штангенциркуля нет, а длина оголенного проводника позволяет сделать его накрутку на карандаш длиной не меньше 1 см, можно использовать данный способ. Все, что нужно – подсчитать витки, которые поместились на отрезке длины 1 см. Диаметр получается делением длины отрезка на витки.

С помощью карандаша и линейки замеры будут не совсем точными
Обратите внимание! Точность измерения будет зависеть от того, как плотно была сделана намотка, и какая у нее длина.
В чем измеряется поперечное сечение
После определения диаметра указанными способами площадь сечения можно определить по формуле или специальной таблице. Измеряется она в квадратных миллиметрах. Данная единица измерения производная согласно единой международной системе измерений.
Вам это будет интересно Чет отличается RJ-11 от RJ-12

Мера измерения
При этом разрез жил всегда круглый.
Формула измерения площади поперечного сечения
Рассчитать поперечное сечение, а именно площадь можно через формулу круга S = π * R2, где первым звеном является площадь круга, вторым — константа Пи 3,14, а третьим — радиус. Принимая во внимание тот факт, что радиус является одной второй диаметра, то формула может быть преобразована по желанию. Рассчитывая площадь, следует использовать диаметр.
Обратите внимание! Чтобы определить сечение многожильного провода, нужно вычислить площадь одной жилы, а затем полученное значение перемножить на количество проводниковых жил.
Определяя диаметр проводника комнатной электропроводки, нужно взять во внимание показатель одновременной максимальной потребительской нагрузки. Принимая в расчет показатель мощности, берется сечение линий, идущих от центра счетчика и вводных автоматов к распределительной коробке. Это места с суммарной нагрузкой всех подсоединенных потребителей. Делать выбор лучше в пользу медного провода с жилами не меньше 6 мм².

Формула для расчета
Поперечным сечением называется площадь среза под углом 90° к оси. Рассчитывать его на проводнике можно штангенциркулем, карандашом, линейкой. Измеряется оно в квадратных миллиметрах. Подсчитывается по специальной формуле, представленной выше. Ничего сложного в этом нет, главное — выбрать самый точный вариант.
Важные измерения
Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.

Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:

- S = 4 * 3,14 * 10²;
- S мяча равна ≈ 1256 см².
Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.
Сектор сферы — это слой между двумя правильными круговыми конусами, имеющими общую вершину в центре шара и общую ось.
Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Источник: italy-expert.ru
Балки подстропильные: виды, поперечное сечение, установка. Подстропильная ферма
Основой конструкции при устройстве кровель выступают стропильные и подстропильные элементы. Несущая система кровельного покрытия – это стропильные балки и фермы. Балки подстропильные являются опорой для стропильных элементов. Они применяются при устройстве покрытий в одноэтажных многопролетных промышленных зданиях, в жилых домах при устройстве мансардных этажей.
Виды подстропильных балок и ферм
Надежность всей кровельной системы в полной мере зависит от прочности и основательности несущей стропильной и подстропильной конструкции. На нее оказывается большое количество разнообразных внешних нагрузок.
Балки подстропильные – это изделия из одного цельного элемента, который принимает внешнюю нагрузку, распределяя ее по всей своей длине. В этом случае наибольшие напряжения возникают по концам балки. Применяется она в балочных стропильных системах устройства кровли.
Подстропильная ферма – это сложная составная конструкция, которая собирается из отдельных стержней, жестко соединенных друг с другом. Нагрузки возникают только в узловых соединениях стержней. Используются такие конструкции в кровельных системах со стропильными фермами.
В зависимости от материала изготовления подстропильные конструкции можно разделить на:
- Железобетонные.
- Стальные.
- Деревянные.
- Армированные деревянные системы.
Железобетонные и стальные балки и фермы наиболее часто используются в строительстве промышленных зданий и сооружений. Деревянные и усиленные арматурой элементы из дерева активно применяются для устройства не только производственных кровель, но и при строительстве крыш в жилых домах.
В промышленном строительстве подстропильными конструкциями перекрывают 12-метровые, 18-метровые, 24-метровые и 30-метровые пролеты между колоннами. При шестиметровом шаге стропильных конструкций подстропильные балочные элементы и фермы служат для них промежуточными опорными элементами.
По виду поперечного сечения балки подразделяются на:
- Прямоугольные.
- Тавровые.
- Двутавровые.
- Коробчатые балки.
В индивидуальном жилищном строительстве конструкции, предназначенные для опоры стропильной системы, применяются не часто. В основном их используют при устройстве мансардных помещений.

Железобетонные подстропильные балки
Железобетонные изделия применяются для устройства кровельных покрытий с небольшим уклоном, а также скатных крыш. Изготавливаются они на заводах ЖБИ, где сразу применяется предварительное напряжение балок стальной арматурой. Виды используемой арматуры:
- Стержни с периодическим профилем упрочненные.
- Проволочные пучки из особо прочной проволоки.
- Витые проволочные пряди.
- Струнная арматура.
По форме различают балки подстропильные с параллельными и не параллельными поясами. Их расчет производится исходя из нагрузки, которую оказывает стропильная балка, опирающаяся точечно на середину подстропильного элемента, и нагрузки от веса самой балки, распределяемого по ее длине. Изделия изготавливаются со строповочными отверстиями, предназначенными для монтажа и подъема, иногда вместо них используются монтажные петли.
Устанавливаются в средних рядах сооружений для опоры стропильных балок и ферм, если ширина их шага 6 метров, а ширина установки средних колонн – 12 метров. Установка подстропильных балок производится на колонны, закрепляются они методом сваривания закладных деталей. В середине балок подстропильных и по их концам выполнены специальные опорные площади с закладными листами и анкерными болтами для установки стропильных конструкций.
Имеют тавровое или двутавровое поперечное сечение с нижней полкой и форму трапеции. Нижняя полка усиливается в местах, где предполагается установка стропильных балок.
По длине балки подстропильные в основном бывают 12-метровые, иногда применяются 18-метровые или 24-метровые изделия. Высота по центру составляет 1,5 метра, в местах опор – 0,6 метра. Ширина нижней полки – 0,7 метра. Должна иметь определенные двутавровая балка размеры. ГОСТ 19425-74.
Подстропильная железобетонная ферма
Железобетонные подстропильные фермы применяются при устройстве скатных кровель. Имеют форму трапеции, у которой два пояса: нижний — горизонтального вида и верхний — ломаной конструкции. На данный момент наиболее актуальными являются безраскосые фермы из сборного железобетона.
Для надежности крепления стропильных ферм опорные участки подстропильных элементов усиливаются. Для установки плит покрытия предусмотрены стойки у опор. Стойки и нижний пояс подстропильной фермы изготавливаются с предварительным напряжением. Для производства используется бетон марок 300-500.
Как и в балочном варианте, в подстропильных фермах для крепления к колоннам и опоры предусмотрены закладные металлические элементы.
Стальные подстропильные балки
Стальные системы имеют длину 12 метров, 18 метров, 24 метра, могут производиться длиной 48 метров. Конструкционно они аналогичны применяемым стропильным балкам. Состоят из двух поясов: верхнего и нижнего. Верхний опирается на монтажный столик на колонне и крепится к нему болтами. Нижний пояс балки прикрепляется к колонне посредством горизонтальных планок.

Подстропильная стальная ферма
Изготавливаются с параллельными верхним и нижним поясами. Длина унифицирована и составляет 12 метров, 18 метров, 24 метра. В зависимости от вида стропильной фермы, высота подстропильной конструкции может быть 3,13 метра, 3,27 метра или 3,75 метра.
Крепление к колоннам производится при помощи надопорных стоек, на которые опирают стропильные фермы.
В настоящее время в промышленном строительстве стали применяться облегченные стальные варианты изготовления ферм. Например, трубчатые системы или балки с тонкими стенками. Благодаря такой конструкции фермы получаются более легкие, уменьшается расход стали на их изготовление, сокращается срок их монтажа.

Деревянные подстропильные системы
Конструкции из дерева, предназначенные для опоры на них стропильной системы, обладают достаточно большой прочностью и стойкостью ко многим агрессивным воздействиям. Они долговечны при применении их в сооружениях с нормальными режимами по температуре и влажности. В промышленном строительстве они используются в зданиях, где присутствуют неблагоприятные для железобетона и металла среды.
По конструктивному виду различают подстропильные элементы в виде:
Если длина пролетов в здании до 18 метров, то применяется подстропильная балка деревянная. В зданиях, где пролеты достаточно большие – до 30 метров, целесообразнее использование деревянных подстропильных ферм. Арки и рамы из дерева в качестве подстропильных элементов используются не часто.
Деревянная подстропильная балка
В промышленном строительстве чаще всего используются балки, склеенные из досок. Такие конструкции гораздо прочнее и долговечнее, чем цельные изделия, возможно изготовление различных форм подстропильных балок. Изделия из конструкционного клееного бруса получили широкое распространение при устройстве кровельных систем. Цельные круглые бревна могут выдержать более серьезные нагрузки, но они сильно уступают клееному брусу по прочности на изгиб.
Узел стыкования деревянной подстропильной балки можно увидеть на фото ниже.
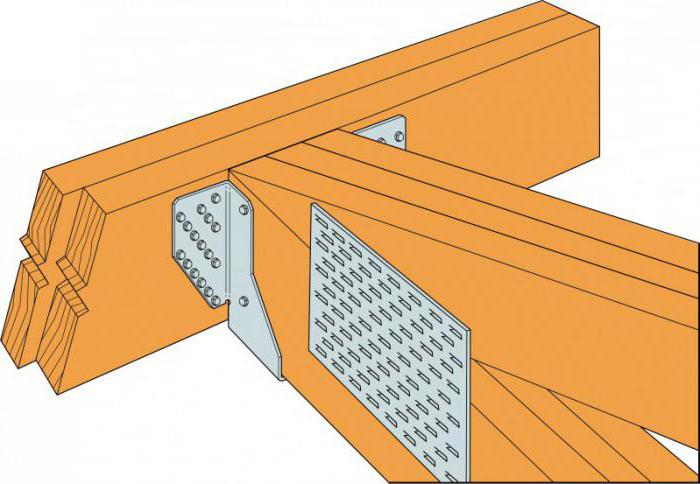
Поперечное сечение балки бывает прямоугольным или двутавровым. Верхний и нижний пояса подстропильной балки могут быть параллельными, либо двускатный верхний пояс и горизонтальный или ломаный нижний пояс. При длине пролета до 15 метров часто используются двутавровые балки со стенками из досок или фанеры и брусковыми ребрами жесткости.

Деревянная подстропильная ферма
Основными материалами для изготовления подстропильных деревянных ферм являются брусья, доски или бревна. Крепление элементов возможно при помощи металлических метизов, пластин. Большое распространение получили клееные деревянные подстропильные фермы. Пояса их изготавливаются сплошными по ширине.
При таком способе изготовления на концах соединительных элементов выполняются нарезные зубчатые шипы и аналогичные им по форме пазы. Клей наносится на всю поверхность стыка, далее детали конструкции прессуются.
Армированные деревянные подстропильные балочные элементы и фермы
Армируются деревянные подстропильные элементы с целью их усиления. В качестве арматуры используются сталь или стеклопластик. Крепится арматурная деталь внутрь деревянной при помощи эпоксидного клея. Иногда используется предварительное напряжение арматуры.
Установка
Установка подстропильных балок и ферм проводится следующим образом. Железобетонные подстропильные балочные элементы и фермы при помощи закладных металлических деталей привариваются непосредственно к оголовкам колонн. Возможно крепление их на болты. Железобетонные консоли или металлические столики на подстропильных изделиях выполняют функцию опорных площадок для несущих стропильных конструкций.
Стальные фермы крепятся к колоннам сбоку к металлическому надколоннику нижним поясом. Его высота составляет 0,7 м. Друг с другом фермы скрепляются верхними поясами. Стропильные фермы опираются на столики подстропильных ферм и на закрепленные на колоннах надколенники.
Деревянные подстропильные балки в устройстве кровель выглядят следующим образом (см. фото).

Установка балок для двускатной крыши
Когда в здании существуют две несущие внутренние стены, стропильная система устанавливается на подстропильные элементы. В этом случае они опираются на лежень, посредством стоек из брусьев, а также внутренние стены. Обычно это две подстропильные балочные конструкции, размещенные вдоль крыши. Применяется такой вариант при высоте от перекрытия до конька крыши от 1,4 метра до 2,5 метра. В этом случае под крышей образуется достаточно свободное пространство, которое можно использовать в качестве мансарды.
Подстропильная балка, или затяжка, может устанавливаться непосредственно на стропилах на расстоянии одной трети высоты от перекрытия до конька. Такой вариант позволяет увеличить объем внутреннего помещения под крышей. Стропильная, подстропильная системы и крыша здесь играют роль внешних стен и покрытия.
Стропильные и подстропильные балки можно увидеть на фото в статье.

В первую очередь, на мауэрлат укладываются крайние подстропильные балки на обе стены дома. При варианте деревянного дома вместо мауэрлата используется верхний венец сруба. Балки должны быть строго параллельными друг другу, проверить это можно, измерив расстояние между их концами по диагонали. Балки ложатся с выступом не менее 0,5 метра за края периметра дома. Если доски по длине меньше, чем требуется для балки, то производится сращивание подстропильных балок.
Затем необходимо натянуть веревки между уложенными балками по обоим краям, и выверить их по уровню. На расстоянии одного метра от крайней устанавливается следующая подстропильная балка. Также ложится доска на противоположной стороне. Обязательно проверяется их горизонтальность. Таким образом укладываются остальные балки подстропильные по всей длине стены.
Чтобы выровнять выступы досок за пределы стен, отмеривается 0,5 метра на каждой крайней балке, протягивается веревка. На средних балках делаются отметки по веревке, лишние концы отпиливаются. Дальше на подстропильную систему устанавливаются несущие стропила.
ГОСТы по подстропильным конструкциям
На изготовление железобетонных подстропильных конструкций распространяется ГОСТ 20372-2015, введенный в действие с 1 января 2017 года. Согласно этому документу, для производства используется тяжелый или легкий конструкционный бетон. Стальные подстропильные фермы производятся согласно ГОСТ 27579-88. Имеет определенные и клееная двутавровая балка размеры. ГОСТ 19425-74.
Источник: fb.ru