Основная цель данной статьи состоит в том, чтобы рассмотреть источники роста теоретической механики как фундаментальной науки, сосредоточив главное внимание на взаимодействиях механики с техническими потребностями общества, обусловленными развитием современной техники.
Ключевые слова
Текст научной работы
В настоящее время теоретическая механика, являясь в большей степени фундаментальной дисциплиной, в свою очередь есть научная основа развития современных отраслей техники. Развитие машиностроения вызвало развитие как теоретической механики, так непосредственно связанных с ней дисциплин: теория механизмов и машин, сопротивление материалов, детали машин.
Несмотря на то, что впервые термин «механика» был введен древним философом Аристотелем, в тоже время его учение о движении тел и равновесии сил имели как правильные суждения, так и ошибочные. Поэтому правильнее было бы считать родоначальником механики Архимеда, труды которого сочетали в себе гениальные открытия и изобретения. В свою очередь бурное развитие теоретической механики как науки можно считать в эпоху Возрождения. На ее развитие как науки повлияли два главных фактора, а именно — это потребности развивающегося человеческого общества, которые в последствие будут обусловлены преимущественно развитием техники и технологий. Вторым фактором развития теоретической механики как фундаментальной науки является абстрактное мышление человека, то есть потребность и способность человеческого разума к созданию и открытию нового в своей жизни.
Термех для чайников. Основы теоретической механики
Теоретическая механика является научным фундаментом в наиболее передовых отраслях, таких как авиастроение и ракетостроение. Под воздействием запросов авиационной и ракетной техники существенно развивались следующие разделы: механика тел переменной массы, теория гироскопических явлений, специальная теория относительности.
Первые теоретические исследования в задачах связанных с движение тел переменной массы принадлежат Д. Бернулли и Л. Эйлеру. Эйлер вывел уравнение поступательного движения объекта переменной массы и уравнение вращательного движения тела переменного состава около неподвижной оси.
Главным в работах Эйлера явилось получение выражения реактивной силы установившегося поступательного движения тела переменной массы и момента реактивных сил относительно данной оси. В работах К.Э. Циолковского главное внимание уделялось проблеме космического полета ракеты.
Он разработал основные принципы создания летательного реактивного аппарата и проанализировал условия межпланетного полета. Исследования движения небесных тел, масса которых меняется из-за падения метеоритов на их поверхность принадлежит И.В. Мещерскому.
Автор решил задачу построения общей теории, на основе которой можно было бы исследовать частные случаи движения тел переменной массы. Важнейшими работами И.В. Мещерского в построении общей теории движения тел переменной массы было рассмотрение одновременного присоединения и исключения частиц от основной движущейся материальной точки и исследование вращения твердого тела переменной массы вокруг неподвижной оси.
Техническая механика
Для понимания гироскопических явлений Л. Эйлером были выведены кинематические и динамические уравнения, описывающие вращение твердого тела около центра масс и неподвижной точки. Ж. Лагранж нашел общее решение уравнения Эйлера для твердого тела, у которого моменты относительно двух главных осей равны, центр масс смещен относительно точки опоры вдоль третьей главной оси.
Позднее в конце девятнадцатого века произошло зарождение гироскопической техники: гирогоризонта, гироскопа направления, гироскопического компаса. В наши дни уже более совершенные гироскопические приборы нашли свое применение в авиационной технике, в частности в самолете амфибии Бе-200ЧС, находящийся на вооружении в подразделениях МЧС России. Самолет оснащен комплексом пилотажно-навигационного оборудования и средств связи, которые обеспечивают навигацию и управление в любых метеоусловиях. Самолет предназначен для доставки в район бедствия спасателей и средств пожаротушения, сдерживание распространения средних и крупных пожаров.
В настоящее время на законах теоретической механики, а именно статики и кинематики строится теория движения пожарного автомобиля, где проводится анализ ряда эксплуатационных свойств: тягово-скоростных, тормозных, устойчивости движения, маневренности, управляемости, плавности хода.
Тяговые силы ведущих колес определяют тягово-скоростные свойства пожарного автомобиля. Тягово-скоростные свойства оцениваются величиной удельной мощности, которая выражается отношением мощности двигателя к полной массе автомобиля.
Сопротивление качению колеса с пневматической шиной по недеформируемой дороге возникает за счет затрат энергии на деформацию шины, напротив сопротивление качению колеса по деформируемой дороге возникает за счет затрат энергии на деформацию грунта и на преодоление сил трения между колесом и грунтом. Сила сопротивлению качению колес пожарного автомобиля является суммой сил сопротивлению качения всех колес и прямо пропорциональна коэффициенту сопротивления качению и нормальной реакции поверхности каждого колеса.
Практически для определения тех или иных эксплуатационных свойств автомобиля одним из основных параметров являются нормальные реакции опорной поверхности колес. Следует отметить, что величины нормальных реакций определяются правилами статики путем составления уравнений равновесия произвольной плоской системы сил.
Источник: novainfo.ru
ОСНОВНЫЕ ПОЛОЖЕНИЯ
Техническая механика — это общетехническая дисциплина, в которой излагаются основы и методика расчета наиболее распространенных элементов различных конструкций на прочность, жесткость и устойчивость.
Прочностью называется способность материала или конструкции воспринимать различные воздействия (нагрузки, температурные перепады, просадки грунтов и т.п.), не разрушаясь и не претерпевая беспрепятственного деформирования. Под разрушением подразумевается полное нарушение целостности тела (конструктивного элемента) вследствие накопления повреждений и развития трещин (рис. 1.1, а).

Техническая механика, будучи начальной ступенью сопротивления материалов, по своему содержанию примыкает к разделу механики, именуемому механикой деформируемого твердого тела, где рассматриваются законы равновесия и движения твердых тел в условиях их деформирования при различных воздействиях (нагрузках). Из этой науки и техническая механика, и сопротивление материалов заимствуют общую методологию и математически более точные и обоснованные решения отдельных задач. В то же время обе дисциплины опираются на методы и уравнения механики абсолютно твердого тела (теоретической механики), где постановка вопроса о расчете на прочность лишена смысла, поскольку в самой терминологии заложена идея неразрушимости и отсутствия каких бы то ни было деформаций. Поскольку все твердые тела (конструктивные элементы) в той или иной степени деформируемы, т.е. способны под нагрузкой изменять свои геометрические размеры и форму, техническую механику можно рассматривать как следующий после теоретической механики шаг на пути приближения к расчету реальных конструкций и сооружений.
В случаях, когда деформации тела несущественны и ими можно пренебречь, выводы теоретической механики оказываются точными и вполне достаточными, например опорные реакции статически определимых балок находят из уравнений статики, предполагая, что эти балки абсолютно недеформируемы. При расчете грузоподъемных механизмов обычно пренебрегают деформациями звеньев, которые изготовляют весьма жесткими, поэтому скорости и ускорения, вычисленные по правилам кинематики, точно соответствуют действительным. В то же время существует обширный класс систем, которые принципиально не могут быть рассчитаны без рассмотрения их в деформированном состоянии (так называемые статически неопределимые системы).
Деформирование нагруженной конструкции и ее элементов обусловливает перемещение их отдельных точек (сечений). Так, элемент, изображенный на рис. 1.1, б, получает вертикальные перемещения. При некотором значении нагрузки максимальное перемещение может воспрепятствовать нормальной эксплуатации элемента, хотя его прочность еще не исчерпана.
В таком случае считают, что элемент (конструкция) имеет недостаточную жесткость. Следовательно, жесткость можно характеризовать как способность конструктивного элемента воспринимать воздействие без существенного изменения формы и геометрических размеров.
Помимо прочности и жесткости конструкции и их элементы должны обладать устойчивостью, т.е. способностью сохранять под нагрузкой первоначальную форму равновесия. Если малое приращение нагрузки вызывает сильное нарастание отклонения тела (элемента) от положения равновесия — выпучивание, рис. 1.1, в), то утверждают, что тело (элемент) потеряло устойчивость. Проблема обеспечения устойчивости возникает при расчете тонких сжатых элементов, и ей уделяется особое внимание, так как потеря устойчивости может происходить при нагрузках, безопасных с точки зрения прочности или жесткости.
Техническая механика играет важную роль в инженерно-строительном образовании, являясь связующим звеном между теоретическими науками (математикой, физикой, теоретической механикой и др.) и специальными дисциплинами (такими как сопротивление материалов в широком понимании, строительная механика, испытание сооружений, строительные конструкции и т.д.), связанными с расчетом и проектированием надежных и экономичных строительных конструкций.
Надежной считается конструкция, которая сохраняет свою эксплуатационную способность (прочность, жесткость, устойчивость) в течение заранее предусмотренного промежутка времени. Нарушение возможности эксплуатировать конструкцию называется отказом. Таким образом, надежность представляет собой способность конструкции или ее отдельных элементов безотказно выполнять свои функции в течение установленного срока службы.
Надежность и экономичность являются, по существу, противоположными понятиями. Важнейшее требование строительной техники — обеспечение надежности сооружения при наименьшей затрате материала — содержит в себе противоречие, поскольку повышение уровня надежности достигается чаще всего увеличением поперечных размеров конструктивных элементов, в то время как экономия материала заставляет стремиться к уменьшению тех же самых размеров. В этом проявляется один из законов диалектики — закон единства и борьбы противоположностей.
Техническая механика помогает разрешить данное противоречие, позволяя установить в каждом конкретном случае оптимальные размеры, при которых надежность обеспечивается без излишних запасов, удовлетворяя экономической стороне вопроса.
Таким образом, основными задачами технической механики являются обоснование, разработка и совершенствование методов расчета наиболее распространенных элементов конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности и экономичности.
Для решения этой задачи теоретическая часть дисциплины тесно увязывается с экспериментальной. Опыт позволяет изучить в сравнительно простых условиях механические свойства конструкционных материалов путем лабораторных испытаний специальных образцов.
В дальнейшем опытные данные используют в теории для расчета конструктивных элементов из того же материала в любых, даже самых сложных условиях нагружения. Кроме того, теория указывает, в каком направлении необходимо вести экспериментальное исследование. Опыт, в свою очередь, позволяет проверить справедливость основных теоретических положений и расчетных формул. Для технической дисциплины это особенно важно, так как необходимость доведения каждого расчета до конечного числового результата заставляет прибегать к различным упрощающим предпосылкам и допущениям, которые требуют экспериментального подтверждения.
Источник: studref.com
Роль и значение технической механики в строительстве
Учебная дисциплина «Техническая механика», изучаемая студентами Каменского агротехнического техникума в пределах рабочих программ для технических специальностей, включает следующие разделы:
Теоретическая механика
Раздел «Теоретическая механика» состоит из подразделов:

«Статика» является частью Теоретической механики, изучающей условия, при которых тело находится в равновесии. При этом равновесием считается такое состояние тела, когда оно находится в покое или движется прямолинейно и равномерно.
Методы и приемы, применяемые для решения задач Статики, позволяют определить внешние силовые факторы, благодаря которым тело находится в состоянии равновесия, т. е. по известным значениям внешних сил или моментов, приложенных к телу, осуществить расчет неизвестных силовых факторов (сил, моментов), воздействующих на данное тело.
Выполнение таких расчетов необходимо для осуществления оценки работоспособности конструкций различных сооружений или механизмов при помощи методов и приемов, применяемых в науке «Сопротивление материалов».
«Кинематика» является частью Теоретической механики, и изучает законы движения материальных тел без учета силовых факторов, вызывающих это движение, т. е. с геометрической точки зрения.
Задачи Кинематики сводятся к определению положения тела в пространстве относительно какой-либо системы отсчета в определенный момент времени или через временной промежуток.
Методы и приемы, применяемые при решении задач Кинематики, позволяют производить кинематические расчеты сложных механизмов машин, в которых отдельные детали и узлы совершают относительные перемещения при работе.
«Динамика», в отличие от Кинематики, изучает законы движения материальных тел с учетом силовых факторов, вызывающих это движение.
Методы и приемы, применяемые в Динамике, позволяют производить расчеты движения и перемещения деталей, узлов и механизмов машин, вызываемых приложенными нагрузками и реакциями.
Сопротивление материалов
Детали и механизмы машин
Раздел «Детали и механизмы машин» является прикладным разделом Технической механики. Он изучает возможность практического применения методов и приемов Теоретической механики и Сопротивления материалов при конструировании и проектировании машин, механизмов, сооружений и других инженерных конструкций.
Структура раздела «Детали машин» складывается из составных частей, включающих основные понятия о надежности и работоспособности машин и механизмов, классификацию видов соединений деталей, их свойства и особенности с точки зрения сопротивления материалов, типы и виды механизмов (муфты, опоры, передачи, редукторы и т. п.), а также изучение методов расчета соединений и механизмов по основным критериям работоспособности.
В высших технических учебных заведениях разделы «Сопромат» и «Детали машин» выделены в отдельные предметы, изучаемые студентами по углубленным программам. Обучающимся техническим специальностям среднего профессионального образования (СПО) эти предметы обычно преподаются по упрощенным программам и объединяются в разделы общего курса Технической механики.
Билеты для проверки усвоения знаний при промежуточной аттестации по разделу «Детали машин» можно скачать здесь (документ в формате Word, 600 кБ)
Методические рекомендации и контрольные задания для студентов заочных отделений технических и машиностроительных специальностей:
Примечание: Документы размещены в формате Word, и могут быть сохранены на компьютере или распечатаны на принтере.
Экзаменационные вопросы по Технической механике для студентов:
Предмет и задачи строительной механики
Строительной механикой в широком смысле называется наука о методах расчета сооружений на прочность, жесткость и устойчивость. К ней относятся следующие дисциплины: сопротивление материалов, строительная механика стержневых систем, строительная механика пластин и оболочек, теория упругости, теория пластичности и теория ползучести.
Сопротивление материалов рассматривает вопросы прочности, жесткости и устойчивости отдельных элементов сооружения.
Строительная механика (или теория сооружений) занимается расчетом сложных конструктивных форм и сооружений в целом.
Строительная механика делится на разделы:
а) статика сооружений, изучающая расчеты на прочность при действии статической нагрузки (в том числе и подвижной);
б) динамика сооружений;
в) теория устойчивости сооружений.
Теория упругости, теория пластичности и теория ползучести решают те же задачи расчета сооружений, но в более строгой постановке, т.е. не учитывая некоторые упрощающие допущения, принятые в строительной механике и сопромате.
При этом в курсе теории упругости изучаются случаи, когда в сооружении возникают только упругие деформации, а в курсе теории пластичности – когда возникают и пластические деформации.
В своих решениях строительная механика пользуется методами теоретической механики, графической статики, сопротивления материалов, теории упругости и теории пластичности.
Строительная механика в начальный период развития не была самостоятельной наукой, а сливалась с общей механикой.
Как самостоятельная наука строительная механика стала успешно развиваться лишь в первой половине ХIX в. в связи с начавшимся усиленным строительством мостов, железных дорого, плотин, судов и крупных промышленных сооружений.
Строительная механика является наукой экспериментально-теоретической, т.к. базируется на результатах испытаний сооружений (в натуре и на моделях), опыте их эксплуатации и теоретических исследованиях.
| Д.И. Журавский (1821-1891гг.) при строительстве моста на б. Николаевской ж.д. опытным путем установил метод определения усилий в элементах решетки. Ю.А. Нилендер опытно изучал распределения температуры и температурных напряжений в теле плотины ДнепроГЭСа. |
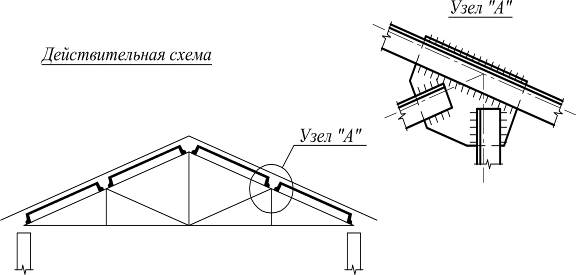
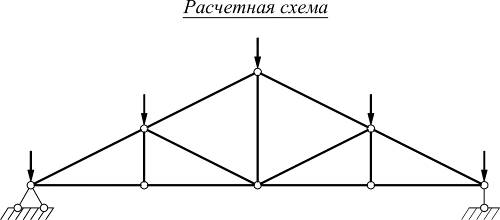
Сложность строгого учета взаимодействия отдельных частей сооружения, всех факторов, влияющих на его поведение, вызывает необходимость рассматривать при расчете не действительное сооружение, а упрощенную схему его, называемую расчетной схемой сооружения.
Расчетные схемы сооружений
Расчетная схема – это упрощенное изображение действительной схемы сооружения. При выборе расчетной схемы следует руководствоваться двумя основными требованиями:
– схема должна возможно более соответствовать действительным условиям работы сооружения;
– схема должна быть возможно более простой, чтобы избежать излишней сложности при расчете.
Классификация расчетных схем сооружений.
I. По геометрическим признакам:
а) стержневые системы – сооружения, составленные из элементов, поперечные размеры которых значительно меньше их длин;
б) пластинки и оболочки – сооружения, составленные из элементов, толщина которых относительно мала по сравнению с шириной и длиной;
в) массивные сооружения, у которых все три размера соизмеримы.
II. В зависимости от типа соединений элементов:
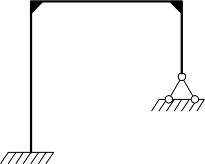
а) системы с жесткими соединениями элементов – рамы;
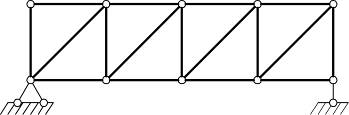
б) системы с шарнирными соединениями элементов в узлах;
в) с комбинированным соединением.

III. По направлению опорных реакций:
а) безраспорные системы – в которых вертикальная нагрузка вызывает только вертикальные опорные реакции;
б) распорные системы – в которых от вертикальной нагрузки возникают вертикальные и горизонтальные опорные реакции.
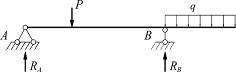 |
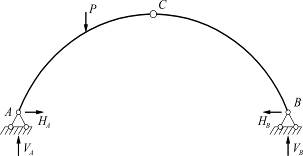 |
| а) безраспорные системы | б) распорные системы |
а) шарнирно-подвижная опора;
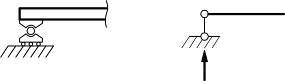 |
Соп=1 |
б) шарнирно-неподвижная опора;
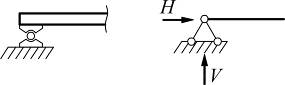 |
Соп=2 |
в) жесткое защемление;
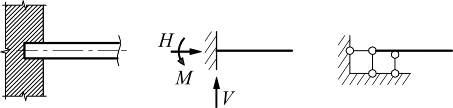 |
Соп=3 |
Кинематический анализ сооружений
Расчетные схемы сооружений могут быть представлены в виде системы геометрически неизменяемых тел, соединенных между собой шарнирами и прикрепленных к земле при помощи опорных устройств.
Эти шарниры и опоры называются кинематическими связями или просто связями, а геометрически неизменяемые тела – дисками.
Геометрически неизменяемой называется такая система соединенных между собой тел, которая не допускает относительного перемещения ее частей без их деформаций.
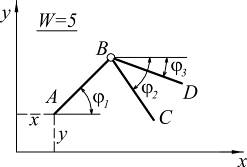
Для уяснения сущности кинематического анализа систем, предварительно рассмотрим отдельный, ничем не связанный плоский диск.
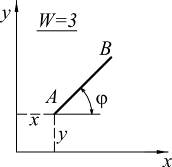 |
Степенью свободы (W) называется количество независимых геометрических параметров, определяющих положение конструкции в пространстве или на плоскости. |
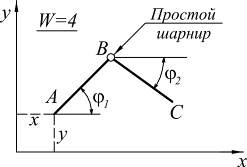 |
Простой шарнир уменьшает степень свободы на |
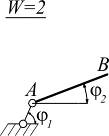 |
Опорный стержень уменьшает степень свободы на |
 |
Шарнир, соединяющий три диска, эквивалентен двум простым шарнирам |
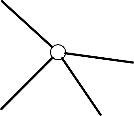 |
Если шарнир соединяет n стержней, то он эквивалентен n-1 простым шарнирам. |
Тогда степень свободы системы в целом определится:
где D – число дисков; Шо – число простых шарниров; Соn – количество опорных связей.
W = 0 – система геометрически неизменяема и статически определима;
W > 0 – система геометрически изменяема;
Примеры: определить степень свободы и провести структурный анализ сооружений:
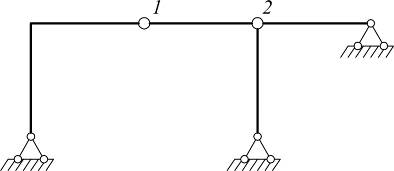 |
система статически определима и геометрически неизменяема |
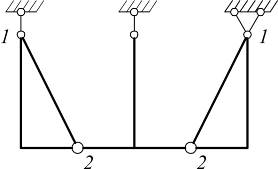 |
система статически неопределима и геометрически неизменяема |
 |
система статически определима, но мгновенно изменяемая |
Дата добавления: 2016-02-04 ; просмотров: 3353 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Цели и задачи строительной механики
Лекция 1
Дополнительная литература
1) Леонтьев Н.Н и др. Основы строительной механики стержневых систем.
2) Анохин Н.Н. Строительная механика в примерах и задачах.
3) Дарков А.В. Строительная механика.
4) Агапов В.П. и др. Строительная механика автомобиля и трактора
5)Агапов В.П. Метод конечных элементов в статике, динамике и устойчивости конструкций.
Цели и задачи строительной механики
Главной целью строительной механики является разработка методов определения усилий в элементах конструкций для последующего анализа прочности этих элементов.
Анализ прочности, в свою очередь, связан с определением напряжений и составлением условий прочности. Если известны усилия в конструкции, то напряжения находятся сравнительно просто, для стержневых элементов они находятся по формулам сопротивления материалов. Анализ прочности по известным напряжениям рассмотрен в курсе сопротивления материалов.
Любая конструкция представляет собой совокупность элементов различных типов (стержней, оболочек, пластин, массивных тел), так или иначе соединенных между собой и подвергающихся различным воздействиям как во время возведения, так и во время эксплуатации.
В данном курсе рассматриваются стержневые конструкции и решаются задачи, связанные с определением усилий при действии статической нагрузки. Раздел строительной механики, связанный с подобными задачами, называется статикой сооружений.
Статическими называютсятакие нагрузки, которые возрастают от нуля до своего конечного значения постепенно и остаются постоянными в течение всего срока эксплуатации сооружения.
Слова «постепенно возрастающие» означают, что нагрузки растут настолько медленно, что в конструкции не возникают инерционные силы.
Отметим, что в качестве строительных сооружений используются неизменяемые и неподвижные конструкции.
Неизменяемыми называются такиеконструкции, взаимные перемещения точек которых возможны только вследствие деформации элементов, в противном случае они являются изменяемыми.
Примеры неизменяемых конструкций приведены на рис.1.1.
Примеры изменяемых конструкций приведены на рис.1.2.
Изменяемые конструкции чаще называют механизмами.
В широком смысле слова конструкцией можно назвать как изменяемую, так и неизменяемую систему. Однако в данном пособии это слово используется в более узком смысле для обозначения неизменяемых систем, каковыми являются несущие конструкции различных объектов техники, а также строительные сооружения.
Неподвижность конструкции (неизменяемость относительно земли) обеспечивается опорными устройствами.
Источник: dom-srub-banya.ru