Строительство санатория имеет форму прямоугольника стороны которого равны

1) Равные фигуры имеют равные площади.
2) Площадь фигуры равна сумме площадей фигур , из которых она состоит.
3) За единицу измерения площади выбирают квадрат , сторона которого равна единичному отрезку .
4) Измерить площадь фигуры — значит подсчитать, сколько единичных квадратов в ней помещается.
5) 1 см 2 — это площадь квадрата со стороной 1 см .
6) 1 дм 2 — это площадь квадрата со стороной 1 дм .
7) Площадь прямоугольника вычисляют по формуле S= a*b , где S — его площадь , a и b — длины соседних сторон, выраженные в одних и тех же единицах .
8) Площадь квадрата вычисляют по формуле S= a 2 , где S — его площадь , a — его сторона .
9) 1 м 2 = 10000 см 2
10) 1 км 2 = 1000000 м 2
11) 1 а = 100 м 2
12) 1 га = 10000 м 2 = 100 а

РЕШАЕМ ЗАДАЧИ

244. Если стороны прмоугольника равны 12 см и 8 см, то его площадь

S = 12*8 = 96 см 2

245. Если сторона квадрата равна 9 дм, то его площадь

S = 9 2 = 81 дм 2

Дачный участок имеет форму прямоугольника … | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 8 | ШКОЛА ПИФАГОРА

246. Заполните пропуски.

1) 6 а = 600 м 2
12 га = 120000 м 2
3 га 42 а = 34200 м 2

2) 7 га = 700 а
6 га 5 а = 605 а
72 000 м 2 = 720 а

3) 4 дм 2 = 400 см 2
4 м 2 = 40000 см 2
2 м 2 35 дм 2 = 23500 см 2

4) 270000 м 2 = 27 га
8000 а = 80 га
2 км 2 = 200 га

247. Сравните величины.

248. Заполните таблицу, где S — площадь прямоугольника, a и b — длины его соседних сторон.

а	3 дм	8 дм	40 см	5 км	36 см	30 м
b	6 см	5 дм	9 дм	4 м	6 дм	4 км
S	180 см 2	40 дм 2	36 дм 2	20 га	2160 см 2	12 а

1) 30 см*6 см = 180 см 2
2) 8 дм*5 дм = 40 дм 2
3) 40 см (4 дм)*9 дм = 36 дм 2
4) 5 км (5000 м)*4 м = 20000 км = 20 га
5) 36 см*6 дм (60 см) = 2160 см 2
6) 30 м*4 км(4000 м) = 120000 м = 12 а

249. Найдите площадь квадрата, периметр которого равен 64 см.

Решение:
1) 64:4 = 16 (см) длина сторон квадрата
2) 16*16 = 256 (см 2 ) площадь квадрата

Ответ: Площадь квадрата 256 см 2 .

ЕГЭ База: задание 10 | Простая и быстрая подготовка к ЕГЭ

250. Поле прмоугольной формы имеет площадь 42 а, его длина равна 70 м. Вычислите периметр поля.

Решение:
42 а = 42000 м 2
1) 42000:70 = 600 (м) ширина поля
2) 2*(70*600) = 2600 (м) периметр поля

Ответ: периметр поля равен 2600 м.

251. На рисунке изображен прямоугольник ABCD, у которого АD=8 см, АВ=4 см. Точка К — середина отрезка АD, точка М — середина отрезка АК, точка F — середина отрезка АВ, точка Е — середина отрезка АF. Чему равна площадь закрашенного прямоугольника?

Ответ: Площадь закрашенного прямоугольника равна 2 см 2 .

252. На рисунке изображены три квадрата. Середины сторон большого квадрата являются вершинами среднего квадрата, а середины сторон среднего квадрата — вершинами маленького квадрата. Площадь маленького квадрата равна 25 см 2 . Чему равна площадь квадрата?

Ответ: площадь квадрата равна 100 см 2

253. Вычислите площадь фигуры, изображенной на рисунке (размеры даны в сантиметрах).

Решение:
(12+3)*6-(2*2*3+2*2) = 74 (см 2 ) или
12*6+2*3-2*2 = 74 (см 2 )

Ответ: площадь фигуры равна 74 см 2 .

254. Заполните цепочку вычислений.

1) 600 а : 300 = 2 а
2) 2 а + 4 а = 6 а
3) 600 м 2 — 120 м 2 = 480 м 2
4) 48000 дм 2 : 800 = 60 дм 2
5) 60 дм 2 — 28 дм 2 = 32 дм 2

255. Сколько надо рулонов обоев, чтобы оклеить ими стену длиной 7 м и высотой 4 м, если длина рулона равна 10 м, а ширина — 50 см?

Решение:
1) 7*4 = 28 (м 2 ) площадь стены
2) 50*1000 = 50000 (см 2 ) = 5 (м 2 ) содержит улон обоев
3) 28:5 = 5 ост.3 (рулоны)

Ответ: 6 рулонов

256. С огорода, который имеет форму приямоугольника со сторонами 50 м и 30 м, собрали 180 ведер картофеля. В одно ведро помещается 8 кг картофеля. Сколько килограммов картофеля собрали с 1 а?

Решение:
1) 50*30 = 1500 (м 2 ) = 15 а — площадь огорода.
2) 180:15 = 12 (ведер) с одного а
3) 12*8 = 96 (кг) с одного а

Ответ: 96 кг с одного а.

257. Длина прямоугольника равна 28 см. На сколько квадратных сантиметров увеличится его площадь, если ширину этого прямоугольника увеличить на 3 см?

Решение:
28*(х+3)-28*х = 28х+28*3-28х = 28*3 = 84 (см 2 )

Ответ: площадь увеличится на 84 см 2 .

258. Во сколько раз увеличится периметр и во сколько раз увеличится площадь прямоугольника, если каждую его сторону увеличить в 3 раза?

Решение:
1) 2*(3а+3b):2(а+b) = 6а+6b:2а+2b = 6(а+b):2(а+b) = 6:2 = 3
2) (3а*3b):(а*b) = 9аb аb = 9

Ответ: в 3 раза; в 9 раз.

259. На рисунке изображен квадрат, разбитый на шесть прямоугольников, сумма периметров которых равна 80 см. Чему равна площадь квадрата?

Источник: matem-gdz.ru

Математика 7 Проверочная работа 1

Математика 7 Проверочная работа 1 — подготовка к Всероссийским проверочным работам (авт. Е.В. Буцко). ВПР Работа № 1 «Линейное уравнение с одной переменной. Отрезок. Луч.

Угол». Цитаты использованы в учебных целях. Ответы адресованы родителям.

ВПР: математика 7 класс. Проверочная работа № 1
«Линейное уравнение с одной переменной. Отрезок. Луч. Угол»

Вариант 1 (образец)

1. Найдите значение выражения 20,6х – 3,8 при х = –7.
2. Найдите значение выражения –3c/11 + d/4, если с = 33, d = –16.
3. Установите соответствие.

1. Выберите целые выражения и запишите в ответе их номера.
   1) 2/21 – 4b; 2) 3,4аb – а/11; 3) 14а + b 2 /a; 4) –а 4 + 7/a; 5) –a 7 /31 – a 2 /7.
2. Решите уравнение –2х + 31 = 12x – 25.
3. Периметр кухни, имеющей форму прямоугольника, равен 15 м. Длина кухни на 1,5 м больше ширины. Найдите длину кухни.
4. На диаграмме, изображённой на рисунке, показано количество однокомнатных, двухкомнатных и трёхкомнатных квартир в доме.
   На сколько трёхкомнатных квартир в доме меньше, чем двухкомнатных, если а = 50?
5. Верно ли утверждение? Уравнение –41 – 13x = –13x – 41 не имеет корней.
6. При каких значениях переменной значение выражения –х/21 + х/7 равно 2/7?
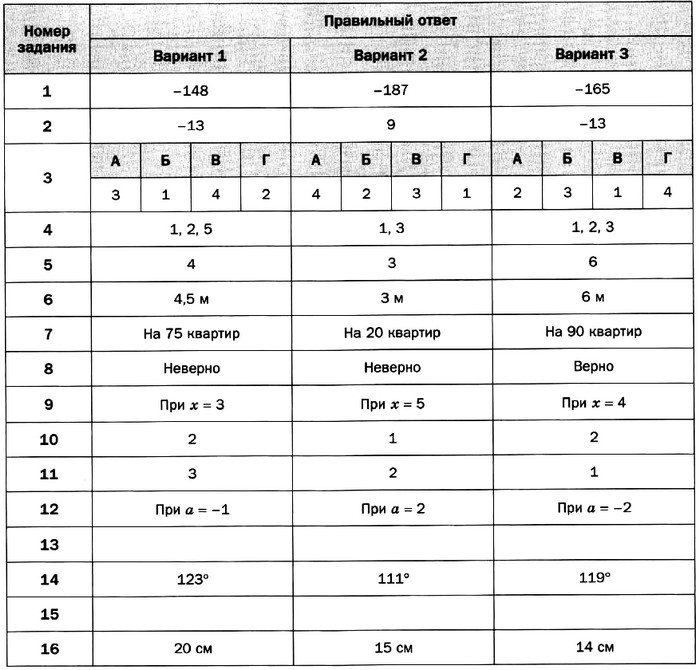
7. Длина отрезка DC больше длины отрезка MN. Длина отрезка АВ меньше длины отрезка MN. А длина отрезка EF не больше длины отрезка АВ. Выберите неверное утверждение и запишите его номер.
   1) Наибольшим из данных отрезков является отрезок DC.
   2) Отрезки EF и АВ равны.
   3) Длина отрезка DC больше длины отрезка АВ.
8. Оксана планировала решать ежедневно по 5 задач, чтобы подготовиться к олимпиаде по физике к определённому сроку. Но она ежедневно решала на 3 задачи больше, чем планировала, и подготовилась к олимпиаде по физике за 3 дня до окончания запланированного срока.
   Пусть Оксана планировала подготовиться к олимпиаде по физике за х дней. Какое из данных уравнений является математической моделью ситуации, описанной в условии задачи?
   1) 8х = 5(х + 3); 2) 5х = 8(х + 3); 3) 5х = 8(х – 3); 4) 8х = 5(х – 3).
   В ответе укажите номер уравнения.
9. При каком значении а уравнение (–4а + 3)х – 47 = –2а имеет корень, равный 7.
10. Длина отрезка MN равна 6 см. Постройте на прямой MN точки, для которых сумма расстояний до концов отрезка MN равна 8 см.
11. На рисунке луч OD является биссектрисой угла СОВ, ∠COB = 114°. Найдите угол AOD.
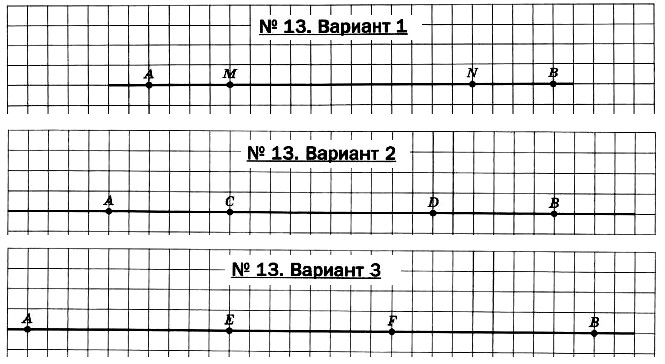
12. Расход воды семьи Павловых в мае составил 6,5 м 3 . В июне семья отдыхала в санатории несколько дней, поэтому расход воды в июне уменьшился на 2,5 м 3 . А в июле расход воды увеличился на 80% по сравнению с июнем.По данному описанию постройте соответствующую диаграмму расхода воды.
13. Периметр треугольника АВС равен 54 см. Сторона ВС составляет 4/5 стороны АВ, сторона АС на 2 см меньше АВ. Найдите длину наибольшей стороны треугольника.

ОТВЕТЫ на проверочную работу

Вы смотрели: Математика 7 Проверочная работа 1 — подготовка к Всероссийским проверочным работам (авт. Е.В. Буцко). ВПР Работа № 1 «Линейное уравнение с одной переменной. Отрезок. Луч. Угол».

Цитаты использованы в учебных целях. Ответы адресованы родителям.

Источник: xn—-8sbuffbhpdbebz1a7m.xn--p1ai

Приведем другое решение.

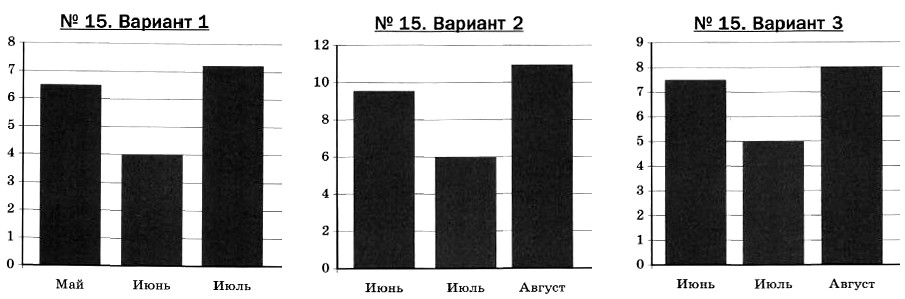
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	Гостиная	Баня	Гараж	Кухня
Цифры

Инна Сергеевна имеет дом с участком. На рисунке приведён план этого участка.

При входе на участок слева находится гараж площадью 15 м 2 , справа расположена баня. Дом находится внутри участка, имеет форму прямоугольника. Сторона каждой клетки на плане равна 1 метру.

Вход в дом осуществляется через стеклянную дверь. Внутри дома расположены: кухня, гостиная, спальня, детская комната, подсобные помещения.

В центре дома находится гостиная, справа — кухня. Спальня и детская имеют равные площади, подсобные помещения обозначены на плане цифрой 7.

Площадка около входа и дорожки вокруг дома выложены плитками размером 1 м × 1 м, на остальной территории посеяна трава.

Решение.

Дом находится внутри участка, имеет форму прямоугольника. В центре дома находится гостиная, справа — кухня. Значит, гостиная отмечена цифрой 3, а кухня отмечена цифрой 4. При входе на участок слева находится гараж площадью 15 м 2 , справа расположена баня. Следовательно, гараж отмечен цифрой 1, а баня отмечена цифрой 2.

Задание 2 № 367682

Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок понадобилось купить, чтобы выложить все дорожки участка и площадку около входа?

Решение.

Заметим, что, поскольку одна плитка имеет площадь 1 м 2 , для площадки около входа понадобится 34 плитки. Для того чтобы выложить все дорожки, понадобится ещё 80 плиток. Значит, всего необходимо

80 + 34 = 114 плиток.

Теперь найдём, сколько упаковок плитки понадобилось:

Следовательно, чтобы выложить все дорожки и площадку около входа понадобится 29 упаковок плитки.

Задание 3 № 367683

Найдите площадь (в м 2 ), которую занимает жилой дом.

Решение.

Заметим, что жилой дом имеет форму прямоугольника. Значит, его площадь равна

м 2 .

Задание 4 № 367686

Найдите расстояние от гаража до бани (расстояние между двумя ближайшими точками по прямой) в метрах.

Решение.

Заметим, что баня с гаражом находятся напротив друг друга. Значит, расстояние между двумя ближайшими точками по прямой бани и гаража равно 11.

Задание 5 № 367687

Инна Сергеевна планирует произвести оклейку стен помещений: детской комнаты и спальни — обоями. Она рассмотрела два варианта: флизелиновые и текстильные обои. Данные о стоимости рулона, площади комнат, расходе обоев на комнаты представлены в таблице. Обдумав оба варианта, Инна Сергеевна решила наклеить текстильные обои. На сколько рублей выгоднее наклеить текстильные обои, чем флизелиновые?

Тип обоев	Стоимость 1 рулона (руб.)	Площадь стен комнат (м 2 )	Расход обоев на 2 комнаты (рулоны)	Стоимость работ по поклейке обоев (руб.)
Флизелиновые	1800	70	7	12 000
Текстильные	2100	70	5	12 500

Решение.

Чтобы поклеить флизелиновые обои, потребуется

рублей.

Чтобы поклеить текстильные обои, потребуется

рублей.

Значит, разница в стоимости составляет рублей.

Задание 6 № 316340

Найдите значение выражения:

Решение.

Последовательно произведём все действия:

Задание 7 № 311380

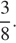
Одна из точек, отмеченных на координатной прямой, соответствует числу Какая это точка?

В ответе укажите номер правильного варианта.

Решение.

Приведём все дроби к одному знаменателю. Получим:

Поскольку точка С соответствует числу

Правильный ответ указан под номером 3.

Задание 8 № 341212

Представьте выражение в виде степени с основанием x.

В ответе укажите номер правильного варианта.

1)

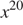
2)

3)

4)

Решение.

Используя формулы получаем:

Правильный ответ указан под номером 1.

Задание 9 № 341402

Решите уравнение

Решение.

Используем свойство пропорции:

Задание 10 № 340463

На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0,1. Вероятность того, что это окажется задача по теме «Параллелограмм», равна 0,6. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.

Решение.

Суммарная вероятность несовместных событий равна сумме вероятностей этих событий: P=0,6 + 0,1 = 0,7.

Задание 11 № 339114

Установите соответствие между функциями и их графиками.

Функции

А)

Б)

В)

Графики

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

A

Б

В

Решение.

Все представленные здесь функции — гиперболы. Общая формула для уравнения гиперболы: , если , то ветви гиперболы располагаются в первой и третьей четвертях, в противном случае — во второй и четвёртой четвертях.

Для того, чтобы отличить гиперболы лежащие в одинаковых четвертях нужно подставить какое-нибудь значение в формулу и проверить, какому графику будет соответствовать полученное значение.

Таким образом, установим соответствие: А — 4, Б — 3, В — 2.

Задание 12 № 341191

Геометрическая прогрессия задана условием Найдите сумму первых её 4 членов.

Решение.

Найдём знаменатель геометрической прогрессии:

Первый член данной прогрессии равен Сумма первых членов геометрической прогрессии может быть найдена по формуле:

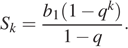
Необходимо найти имеем:

Задание 13 № 311329

Упростите выражение и найдите его значение при . В ответ запишите полученное число.

Решение.

При a = −2, значение полученного выражения равно −2:2 = −1.

Задание 14 № 338396

Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.

Решение.

Найдем расстояние, на котором находится наблюдатель от места удара молнии:

Задание 15 № 316222

Решите неравенство:

В ответе укажите номер правильного варианта.

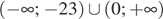
1)

2)

3)

4)

Решение.

Решим неравенство: Корнями уравнения являются числа -23 и 0. Поэтому

Правильный ответ указан под номером 4.

Задание 16 № 132783

Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

Решение.

Сумма противоположных углов вписанного четырехугольника равна 180°, поэтому в условии говорится об односторонних углах. Пусть = , . Тогда ,

Таким образом, искомый угол равен 122°.

Задание 17 № 339483

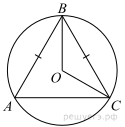
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.

Решение.

Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается. Углы BAC вписанный, он равен половине дуги, на которую он опирается. Поскольку эти углы опираются на одну и ту же дугу, ∠BOC = 2∠BAC. Сумма углов треугольника равна 180°. Треугольник ABC — равнобедренный, углы при его основании равны, поэтому Следовательно, угол BОC = 3°.

Примечание.

Внимательный читатель заметит, что угол В тупой, поэтому центр окружности лежит вне треугольника. Очевидно, что это не влияет на справедливость вышеприведенного решения — задачу можно решить и вовсе без рисунка. Поэтому мы не стали менять тот рисунок, который был дан авторами задания.

Задание 18 № 322861

Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

Решение.

Площадь получившейся фигуры равна разности площадей квадрата и прямоугольника: 6 · 6 − 4 · 2 = 28.

Задание 19 № 352060

Найдите тангенс угла

Решение.

Найдем каждую из сторон треугольника , чтобы показать, что он прямоугольный.

Таким образом,

Задание 20 № 348369

Какое из следующих утверждений верно?

1. Все углы ромба равны.

2. Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.

3. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

В ответ запишите номер выбранного утверждения.

Решение.

Рассмотрим каждое из утверждений:

1. Все углы ромба равны — неверно. Верно только в случае квадрата.

2. Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны — неверно. Стороны квадрата и ромба могут быть равны, однако такие четырёхугольники не равны.

3. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности — верно.

Задание 21 № 338598

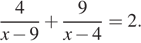
Решите уравнение

Решение.

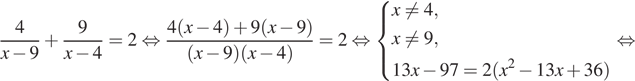
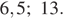
Ответ:

Задание 22 № 126

Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от А. Найдите скорость пешехода, шедшего из А, если известно, что он шёл со скоростью, на 1 км/ч большей, чем пешеход, шедший из В, и сделал в пути получасовую остановку.

Решение.

Пусть скорость пешехода, шедшего из пункта A, равна км/ч, . Тогда скорость пешехода, шедшего из пункта B, равна км/ч.

Составим таблицу по данным задачи:

Скорость, км/ч	Время, ч	Расстояние, км
Пешеход, шедший из A			9
Пешеход, шедший из В			10

Так как пешеход, шедший из A, сделал по пути остановку на ч., а вышли пешеходы одновременно, можно составить следующее уравнение:

Задание 23 № 311565

Постройте график функции и найдите все значения , при которых прямая не имеет с графиком данной функции общих точек.

Решение.

Найдём область определения функции:

и .

Значит, функция определена при .

Поскольку , получаем, что на области определения функция принимает вид . График изображён на рисунке. Прямая не имеет с графиком данной функции общих точек при .

Ответ: .

Задание 24 № 340879

Окружность, вписанная в треугольник ABC , касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 49°, 69° и 62°.

Решение.

Пусть

∠BAC = α , ∠ABC = β , ∠ACB = γ;

∠PKM = 49°, ∠MPK = 69°, ∠KMP = 62°.

По свойству касательных AM = AP, BM = BK , CP = CK . Значит, треугольники AMP, BMK и CPK равнобедренные, откуда получаем:

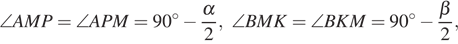
Значит, Аналогично получаем, что и

Решая систему относительно α , β и γ , получаем, что углы треугольника ABC равны 82°, 42°, 56°.

Задание 25 № 341511

Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.

Решение.

Пусть ABCD — трапеция, M и N — середины оснований AD и BC соответвенно.

Пусть AM = MD = a и BN = NC = b, а h — высота трапеции. Тогда площадь каждой из частей, на которые отрезок MN делит трапецию, равна то есть, эти части равновелики.

Приведем другое решение.

Пусть — длина высоты трапеции. Площадь треугольника равна площади треугольника поскольку высоты, проведённые к основаниям и равны, а основания и равны. Аналогично равны площади треугольников и Покажем, что площади четырёхугольников и равны:

Задание 26 № 340359

Основания трапеции относятся как Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?

Решение.

Введём обозначения, как показано на рисунке. Отрезок, проходящий через точку пересечения диагоналей трапеции, равен среднему гармоническому её оснований. Пусть тогда и Поскольку треугольники и подобны, их высоты и , проведенные соответственно к сторонам AD и BC, относятся как . Тем самым, для отношения искомого отношения площадей трапеций EBCF и AEFD имеем:

Ответ:

Источник: studopedia.ru

Задание №16 ЕГЭ по математике базового уровня

В задании №16 базового уровня ЕГЭ по математике нам предстоит столкнуться со стереометрией. Как таковой “стереометрии” мы не встретим, обычно условие задания содержит объемную фигуру, в которой нам необходимо найти какое-либо расстояние. В данном задании необходимо правильно применить пространственное мышление и выбрать нужное сечение, остальные расчеты происходят в плоскости, причем по несложным формулам (теорема Пифагора и т.д.). Какой-либо конкретной теории я пока приводить не буду, а рассмотрю типовые варианты, на которых мы и рассмотрим алгоритмы решения задач данного типа.

Разбор типовых вариантов заданий №16 ЕГЭ по математике базового уровня

Вариант 16МБ1

Радиус основания цилиндра равен 13, а его образующая 18. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12. Найдите площадь этого сечения.

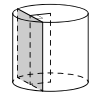
[/su_note]

Алгоритм выполнения:

1. Определить тип фигуры, образующей сечение.
2. Записать формулу для нахождения площади фигуры, образующей сечение.
3. Вычислить недостающие данные.
4. Вычислить искомую площадь сечения.

Решение:

Из рисунка видно, что сечение является прямоугольником, одна из сторон которого образующая цилиндра.

Площадь прямоугольника равна произведению длины на ширину.

Длина прямоугольника – 18, из условия. Осталось вычислить ширину. Сделаем дополнительный чертеж цилиндра сверху:

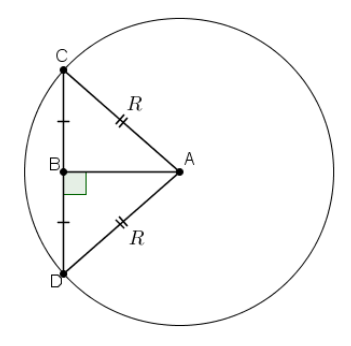
Ширина прямоугольника – CD.

По условию «Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12». Расстояние от точки до прямой – это длина перпендикуляра, проведенного из этой точки на прямую. То есть на чертеже АВ = 12.

СD = СВ + ВD. СВ = ВD

Рассмотрим треугольник ВСА. Треугольник ВСА – прямоугольный.

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

В данном случае СА 2 = СВ 2 + АВ 2

СВ 2 – неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

СВ 2 = СА 2 – АВ 2

СВ = √(13 2 – 12 2 ) = √(169 – 144) = √25 = 5

Для решения задачи необходимо знать СD = СВ + ВD = 5 + 5 = 10

Вычислим искомую площадь сечения.

Вариант 16МБ2

Стороны основания правильной треугольной пирамиды равны 24, а боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды.

Алгоритм выполнения:

1. Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи.
2. Найти площади треугольников.
3. Найти площадь боковой поверхности пирамиды.

Решение:

Проанализируем, какие данные необходимо вычислить для ответа на вопрос задачи.

В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 37, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность.

Найдем площади треугольников.

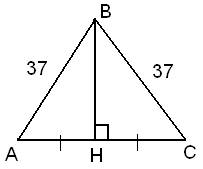
Так как треугольник равнобедренный, то высота BH делит сторону AC пополам, то есть, AH=AC:2=24:2=12. Рассмотрим треугольник АВН. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. В данном случае АВ 2 = ВН 2 + АН 2

ВН 2 – неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

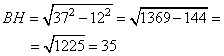
ВН 2 = АВ 2 – АН 2 Следовательно, высота BH, равна:

Площадь треугольника равна половине произведения основания на высоту.

Тогда, площадь треугольника может быть вычислена как

Найдем площадь боковой поверхности пирамиды.

Боковая поверхность пирамиды состоит из трех треугольников. Найдем ее площадь:

Ответ: 1260.

Вариант 16МБ3

Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.

Алгоритм выполнения:

1. Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи.
2. Найти площади треугольников.
3. Найти площадь боковой поверхности пирамиды.

Решение:

Проанализируем, какие данные необходимо вычислить для ответа на вопрос задачи.

В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 17, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность.

Найдем площади треугольников.

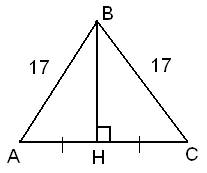
Так как треугольник равнобедренный, то высота BH делит сторону AC пополам, то есть, AH=AC:2=16:2=8.

Рассмотрим треугольник АВН.

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

В данном случае АВ 2 = ВН 2 + АН 2

ВН 2 – неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

ВН 2 = АВ 2 – АН 2

Следовательно, высота BH, равна:

Площадь треугольника равна половине произведения основания на высоту.

Тогда, площадь треугольника может быть вычислена как

Найдем площадь боковой поверхности пирамиды.

Боковая поверхность пирамиды состоит из трех треугольников. Найдем ее площадь:

Ответ: 360.

Вариант 16МБ4

Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.

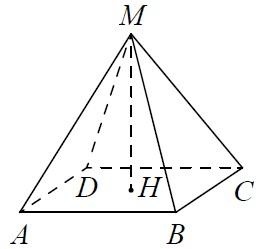
Вспомним формулу площади правильной пирамиды – одна треть от произведения площади основания и высоты.

Площадь основания рассчитываем по формуле площади квадрата – квадрат стороны:

После этого перейдем к нахождению высоты. Для этого нам необходимо рассмотреть прямоугольный (так как основание перпендикулярно высоте) треугольник AMH. AH – половина диагонали квадрата, которая равна √2 его стороны, то есть в нашем случае диагональ равна 4√2, ну а половина – AH = 2√2. Зная гипотенузу и один из катетов, найдем высоту:

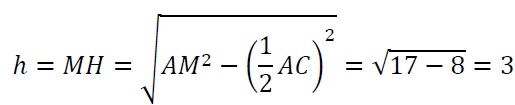
После этого легко вычисляем объем:

V = 1/3 • 16 •3 = 16

Вариант 16МБ5

В треугольной пирамиде АВСD ребра АВ, АС и АD взаимно перпендикулярны. Найдите объем этой пирамиды, если АВ=2, АС=15 и AD=11.

Алгоритм выполнения

1. Записываем формулу для определения объема пирамиды.
2. Находим площадь основания по формуле для площади прямоугольного треугольника.
3. Показываем, что высота пирамиды совпадает с ребром AD. Вычисляем искомый объем.

Решение:

Т.к. в основании пирамиды лежит прямоугольный треугольник с катетами АВ и АС (по условию АВ перпендикулярно АС), то Sосн=АВ·АС/2.

Т.к. AD перпендикулярно АВ и АС и пересекается с ними в одной точке, то (по признаку перпендикулярности прямой и плоскости) AD перпендикулярно плоскости основания пирамиды.

Значит AD – высота пирамиды. Т.е. Н=AD=11.

Вариант 16МБ6

Сторона основания правильной треугольной призмы АВСА1В1С1 равна 2, а высота этой призмы равна 4√3. Найдите объем призмы АВСА1В1С1.

Алгоритм выполнения

1. Находим площадь основы призмы через формулу для площади правильного треугольника.
2. Записываем формулу для объема призмы. Подставляем в нее числовые данные, вычисляем искомую величину.

Решение:

Площадь правильного треугольника равна:

Здесь а – сторона основания призмы.

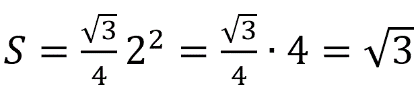
Объем призмы: V=Sh, где h – высота призмы, S– площадь ее основания (в нашем случае – площадь правильного треугольника, лежащего в основании).

Вариант 16МБ7

Объем конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса.

Алгоритм выполнения

1. Записываем формулу для объема конуса. Из нее выражаем площадь основания.
2. Площадь основания расписываем по формуле площади круга, поскольку именно круг лежит в основании конуса.
3. Из этих двух формул выражаем искомую величину. Вычисляем ее.

Решение:

Объем конуса равен:

Площадь круга составляет:

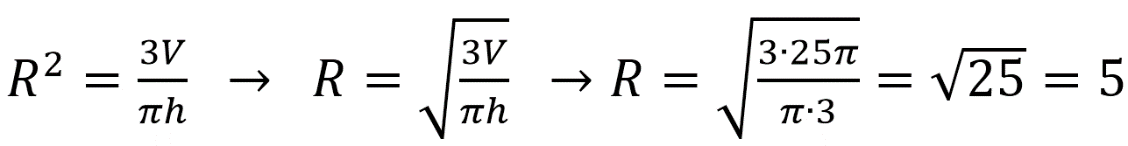
Вариант 16МБ8

Радиус основания цилиндра равен 15, а его образующая равна 14. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12. Найдите площадь этого сечения.

Алгоритм выполнения

1. Определяем, что образующая цилиндра – это одна из сторон сечения-прямоугольника. Вводим обозначения для точек, которые необходимы для выполнения расчетов. Получаем, что образующая – это отрезок DK.
2. Делаем дополнительное построение – соединяем точки О и А в основании цилиндра. Получаем прямоугольный ∆АВО.
3. Из ∆АВО по т.Пифагора находим значение АВ. Этот отрезок – половина AD. Отсюда находим AD.
4. Зная величину DK и AD, вычисляем площадь сечения-прямоугольника.

Решение:

Поскольку образующая цилиндра и его высота совпадают, то DK=14. Это – одна из сторон прямоугольника, форму которого и имеет сечение.

Найдем 2-ю сторону этого прямоугольника. Из прямоугольного ∆АВО по т.Пифагора АО 2 =АВ 2 +ВО 2 .

АО – радиус основания, поэтому АО=15. ВО=12, поскольку ВО – это расстояние от оси до плоскости сечения.

Площадь сечения равна:

Вариант 16МБ9

В прямоугольном параллелепипеде ABCDA1B1C1D1 ребра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √34. Найдите объем параллелепипеда ABCDA1B1C1D1.

Алгоритм выполнения

Решение:

Т.к. ABCDA1B1C1D1 параллелепипед, то угол А1АD равен 90 0 . Поэтому ∆А1АD – прямоугольный. Тогда по т.Пифагора А1А 2 +AD 2 =A1D 2 . Отсюда получаем:

Объем параллелепипеда найдем по формуле:

Вариант 16МБ10

Стороны основания правильной треугольной пирамиды равны 16, а боковые ребра равны 17. Найдите площадь боковой поверхности этой пирамиды.

Алгоритм выполнения

1. Записываем формулу для площади боковой поверхности через периметр основания и апофему.
2. Находим периметр треугольника, лежащего в основании пирамиды.
3. Доказываем, что апофема является не только высотой, но и медианой для боковой стороны пирамиды.
4. Из прямоугольного треугольника, образованного апофемой, боковым ребром и половиной стороны основания, по т.Пифагора находим величину апофемы.
5. Вычисляем площадь боковой поверхности пирамиды.

Решение:

Площадь боковой поверхности пирамиды равна:

Находим периметр основания:

Т.к. пирамида правильная, то ее боковые грани – равнобедренные треугольники. Тогда апофема, которая является высотой боковой грани, проведенной к основанию, является еще и медианой. Значит, SB – медиана и АВ=АС/2=16/2=8.

Из прямоугольного ∆ABS по т.Пифагора АВ 2 +SB 2 =AS 2 .

Вариант 16МБ11

Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 8, а боковое ребро равно √41.

Алгоритм выполнения

1. Записываем формулу для объема пирамиды через площадь ее основания и высоту.
2. Находим площадь основания, учитывая, что в основании пирамиды лежит квадрат.
3. Находим диагональ квадрата, лежащего в основании, как гипотенузу из ∆АВС. Используем для этого т.Пифагора Делим полученную величину пополам.
4. Из треугольника, построенного на половине диагонали основания, высоте пирамиды и ее боковом ребре, по т.Пифагора определяем высоту.
5. Вычисляем объем.

Решение:

Т.к. пирамида правильная, то четырехугольник в ее основании – это квадрат. Поэтому Sосн=а 2 , где а – сторона основания.

Из прямоугольного ∆АВС по т.Пифагора АС 2 =АВ 2 +ВС 2 .

Из прямоугольного ∆АКS по т.Пифагора AS 2 =AK 2 +SK 2 .

Значит, объем пирамиды составляет:

Вариант 16МБ12

Два ребра прямоугольного параллелепипеда равны 8 и 5, а объем параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.

Алгоритм выполнения

1. Записываем формулу для объема прямоугольного параллелепипеда. Из нее выражаем 3-е (неизвестное) ребро. Вычисляем величину этого ребра.
2. Записываем формулу для площади поверхности. Подставляем в него числовые данные, находим искомое значение.

Решение:

Объем прямоугольного параллелепипеда равен:

V=abc, где a, b, c – ребра. Будем считать, что a и b нам известны, а с – неизвестно.

Тогда из этой формулы:

Площадь поверхности прямоугольного параллелепипеда вычисляется так:

Вариант 16МБ13

Объем конуса равен 24π, а радиус его основания равен 2. Найдите высоту конуса.

Алгоритм выполнения

1. Записываем формулу для объема конуса. Из нее выражаем высоту.
2. Записываем формулу для площади круга, лежащего в основе конуса. Вычисляем эту площадь.
3. Подставляем числовые данные в формулу для объема, вычисляем искомую величину.

Решение:

Объем конуса составляет:

.

Площадь основания (как площадь круга) равна:

Тогда высота конуса:

Вариант 16МБ14

Основанием четырехугольной пирамиды является прямоугольник со сторонами 3 и 12. Найдите высоту этой пирамиды, если ее объем равен 60.

Алгоритм выполнения

1. Записываем формулу для объема пирамиды через площадь ее основания и высоту. Из нее выражаем высоту.
2. Находим площадь основы-прямоугольника.
3. Подставляем числовые данные в формулу для высоты, вычисляем искомую величину.

Решение:

Объем пирамиды вычисляется так:

Отсюда:

Sосн=ab, a и b – стороны прямоугольника, лежащего в основе пирамиды.

Источник: spadilo.ru