Сколько существует человечество, столько существует необходимость в транспортировке грузов. В древние времена это делалось на телегах, запряженных лошадьми, или на кораблях. Сегодня для этой цели используются громадные грузовые машины, все те же корабли и самолеты. Прогресс дошел до того, что практически каждый человек в любой точке мира может заказать товар, и он будет доставлен ему самое позднее через месяц.
Однако заказывая что-либо, стоить учитывать не только цену товара, но и стоимость его транспортировки к покупателю. А для этого в первую очередь необходимо знать его объемный вес. Но иногда покупатели путают обычный вес товара с его объемным весом, в результате стоимость заказа оказывается значительно выше, чем предполагалось. Именно поэтому, чтобы не попадать впросак, каждому человеку необходимо знать, как рассчитать объем груза. Что это такое, и чем отличается от обычного веса?
Что такое объемный вес груза
Иногда его называют габаритным весом. Это математическая величина, отражающая количество пространства, занимаемого данным предметом. Этот параметр широко используется транспортными компаниями. Понятие «объемный вес» близко связано с понятием «плотность». В большинстве случаев менее плотные грузы могут занимать больше пространства, чем более плотные.
#1 Физический объем и производительность в MS Project

К примеру, некий человек захотел утеплить свой дом снаружи. Для этого ему необходимы блоки из пенопласта. Поискав в Интернете, он обнаружил, что в Китае они стоят в несколько раз дешевле, чем в его родном городе. Вспомнив, что пенопласт — материал довольно легкий, а значит, больших доплат за вес не предвидится, он заказал нужное ему количество материала. Вот только когда товар прибыл, доплата за вес значительно превысила ожидания, так как заказчик не учел объемный вес заказа, а опирался только на фактический.
Физический, объемный и удельный вес
Прежде чем разобраться с тем, как рассчитать объем груза, необходимо уяснить, чем объемный вес отличается от фактического и что такое удельный вес.
Фактический, или физический, вес – это реальная масса предмета, которую показывают весы. Измеряется он, как правило, в килограммах (при больших количествах в тоннах и центнерах). Объемный вес (объем груза) также измеряется в килограммах, хотя данная величина измеряется в м 3 . Как правило, при расчете стоимости доставки товара указывается тот вес, который больше.

По общепринятым во всем мире правилам расчета массы груза, если в одном м 3 помещается 167 кг груза, данный вес считается физическим, если 1 м 3 груза весит меньше этой цифры – он объемный.
Также при транспортировании используется понятие «удельный вес». Он обозначает соотношение объема груза с его фактическим весом и измеряется в тоннах. В зависимости от материала, из которого состоит груз, он бывает разным.
MS Project и физический объем — Как расчитать график, зная физический объем и производительность
На основе удельного веса выделяется три вида грузов:
- объемный — объем груза превышает его вес;
- тяжелый — фактический вес превышает объемный;
- дедвейтный — фактический и объемный вес приблизительно равны.
Как рассчитать объем груза
Чтобы узнать объем предмета, его высоту умножают на ширину и длину. В случае с расчетом объемного веса этот принцип тоже актуален. Однако если применить этот вид вычисления, получится габаритный размер в кубических метрах, а для расчета отправления нужны килограммы. Поэтому, проводя расчеты объемного веса, нужно использовать специально разработанную для этого формулу, которая используется перевозчиками во всем мире.
Формула объема
Объемный вес груза высчитывается по формуле:
(длина груза (см/м) х ширина груза (см/м) х высота груза (см/м) )/5000.
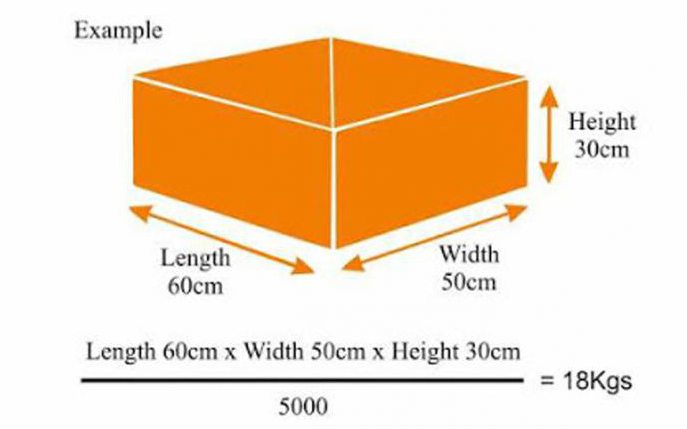
Но стоит помнить, что измеряя предметы нестандартной формы, точкой отсчета измерения является самая длинная деталь, даже если она занимает немного места.
Допустим, необходимо переслать в другой город подростковый велосипед с фактическим весом в 30 кг. Однако, проведя его измерения, обнаружим, что длина велосипеда – 145 см, высота – 95 см, а ширина — 55 см. В действительности велосипед не является столь широким, однако, измерив его самую широкую деталь – руль, его ширину принимаем как ширину всего велосипеда.
Далее нужно рассчитать объем груза (в м3, как правило объемный вес не рассчитывается, чаще всего используют либо см 3, либо кг), для этого (145 х 55 х 95) /5000 = 151,525 (кг). Поскольку объемный вес превышает фактический, при расчете стоимости доставки используют его. Таким образом, доставка такого велосипеда, исходя из его объемного веса, будет почти в пять раз дороже, чем пересылка такой же посылки правильной формы. Так что после проведения вычислений стоит задуматься, есть ли смысл пересылать данный груз вообще, или проще будет разобрать его на детали, тем самым уменьшив объем, а следовательно, и стоимость доставки.
Стоит упомянуть, что число 5000 – это универсальный делитель, принятый многими транспортными компаниями всего мира. В редких случаях он бывает 4000 или 6000. Однако это редкость, кроме того, компании, использующие другой коэффициент, указывают это в сопроводительных документах и на сайтах. Так, зная формулу расчета, можно будет просто заменить делитель.
В современном мире, с его глобализацией и компьютеризацией, владение информацией о том, как рассчитать объем груза, становится таким же необходимым, как и знание того, сколько грамм в килограмме и сколько метров в километре. Многие заблуждаются, полагая, что умение вычислять объемный вес отправления нужно только деловым людям. На самом деле это нужно как студентам, заказывающим по Интернету детали для своего компьютера или велосипеда, так и домохозяйкам, покупающим через Интернет памперсы или одежду. Поэтому, чтобы не попасть в неприятную ситуацию, каждому стоит запомнить способ расчета объема груза.
Источник: www.syl.ru
Что такое «объемный вес»?
Для перевозки груза (именно для перемещения груза, его транспортировки) важнейшими его характеристиками являются:
- физический (фактический) вес — вес, определяемый при взвешивании груза; вес нетто, т.е. вес с тарой и упаковкой;
- фактический и объемный вес.
Важно понимать, что грузоперевозка 100 кг синтепона и 100 кг металлического листа будет стоить по-разному! Ведь любой транспорт имеет лимиты не только по весу, но и по полезному объему. Т.е. на нашем примере это может быть для синтепона 3 м³, а для листа 0,5 м³. Что делать? Считать по весу или по объему?
А если в одной сборной поставке едет и объемный и тяжелый груз одновременно?
Для стандартизации, для удобства оценки стоимости перевозки все-таки принято тарифы рассчитывать за кг груза. Поэтому для расчета стоимости перевозки всегда ведут специальный расчет объемного веса груза, он зависит от эталонного веса кг/1 м³. Но, как это ни прискорбно для считающего, этот эталон не один в природе. Например, для авиаперевозок он один, и даже каждый грузоперевозчик может применять свой собственный эталон для расчета объемного веса.
Объемный вес — это расчетная величина, отражающая плотность груза.
Обычно менее плотный предмет занимает больший объем по сравнению с более плотным при том же весе. Объемный (еще его называют габаритный) вес вычисляется через эталон и сравнивается с фактическим весом, чтобы установить, какой из них больше. Больший вес и используется для расчета стоимости перевозки. Для расчета объемного веса необходимо знать «эталонный объемный вес».
Например, наш партнер в Германии ITG применяет 300 кг/м³ (300 кг в одном кубическом метре. А для авиаперевозок объемный вес равен 167 кг.
Пример: вес груза 130 кг и примерный объем полкуба (0,5 м³). Необходимо вычислить объемный вес указанного груза и сравнить его с «эталонным» от ITG.
Для корректного сравнения надо рассчитать «эталонный» объемный вес для такого же объема груза, т.е. для 0,5 м³: 0,5 м³×300 кг = 150 кг (при необходимости округляем до 0,5 кг).
Итак, сравниваем 150 кг («эталонный объемный вес») и физический вес груза 130 кг. 150 больше 130, потому расчет стоимости перевозки будет вестись исходя из 150 кг.
Из расчетов видно, как важно знать не примерный вес или объем, а точный. Например, из нашего примера видно, что если клиент ошибся в определении объема и фактический объем составлял 0,4 м³, то расчет стоимости велся бы за 130 кг, а не за 150 кг (0,4м³×300 кг = 120 кг < 130 кг).
Доставка из Европы — в России уже через 5-7 дней!
Вот почему мы всегда дотошно запрашиваем у клиентов подробные характеристики груза, вес и объем. Ошибка в определении размеров, объема и веса груза может привести к тому, что в счете стоимость либо будет завышена; либо занижена и клиенту придется доплачивать, если ранее клиент указал неверные данные для расчетов (неверно указанный вес также грозит штрафами при взвешивании грузов при переходе .
Источник: proft.ru
Физические измерения
С давних пор человеку приходилось что-нибудь измерять и вычислять. Сначала люди ограничивались тем, что определяли: больше или меньше одно тело другого или они примерно равны. А как рассказать о размерах тела, если его нет перед глазами?
План урока:
Измерить – значит, сравнить
На помощь человеку приходят числа, используя которые можно было сравнить предметы по величине. Так в одном известном мультфильме длину удава измеряли в «попугаях», сравнивая величину удава с длиной попугая.
Из мультфильма «38 попугаев».
Длина удава 38 «попугаев». Понятно, что удав в 38 раз длиннее попугая. Но попугаи бывают разными. Если взять другого попугая, тот же удав будет, например, 45 «попугаев». Что делать?
Нужно найти тело, принимаемое за единицу измерения, с которой сравниваются другие тела.
В практической деятельности человеку приходится часто измерять длину, массу и время. В разных странах вводились разные единицы измерения этих величин. Существовали такие единицы, как «лошадиная сила», локоть, бочка. Но ведь и локоть, и бочка могут быть разными, поэтому о точности выполнения работы говорилось приблизительно.
Сравнивать нужно только однородные физические величины. Длину тела нужно сравнивать с длиной другого тела, а массу тела – только с массой другого тела, принятого за единицу измерения. Так массу удава из мультфильма можно было сравнить с массой обезьянки. Удав имеет массу 195 «обезьянок». Что бы это значило?
Выход был найден, когда ввели систему единиц СИ. Чтобы измерить любую величину, нужно сравнить ее с однородной величиной, принятой за единицу. Как же выбирают эти единицы?
Наиболее распространено измерение длины, размеров пройденного пути, расстояния. Все эти величины измеряются в метрах. Один метр получили следующим образом. Взяли одну сорока миллионную часть меридиана, который проходит через столицу Франции – Париж. Длину этой части и приняли за 1 метр.
На стержне, изготовленном из иридия и платины, нанесли два деления, расстояние между которыми равно одному метру. Такой сплав меньше всего подвержен температурному влиянию, которое может изменить длину тела. Это стержень и есть эталон длины, с которым сравнивают единицу длины во многих странах мира. Метровые линейки – это многочисленные копии эталона, которыми как раз и можно пользоваться.
Эталон длины
Первый эталон метра был изготовлен из латуни в 1795 г. С 1960 г. используется изготовленный с помощью электронных технологий эталон из сплава иридия и платины.
Существует и эталон массы, равный одному килограмму. Он также изготовлен из сплава иридия и платины.
Эталоны длины и массы хранятся в г. Севр, вблизи Парижа, где располагается Международная палата мер и весов. В 1960 году метр начали сравнивать с величинами, относящимися к разделу «Световые явления». Подробности о свете изучаются в старших классах.
Со светом связана и единица времени – 1 секунда. А до 1960 года (год введения СИ) за основу подсчета времени брали время оборота Земли вокруг Солнца – 1 год, который по календарю состоит из 12 месяцев. Месяцы делятся на сутки – время полного оборота Земли вокруг своей оси, сутки — 24 часа, в каждом из которых 60 минут. А одна шестидесятая часть минуты и есть одна секунда.
Время «хранят» при помощи очень точных часов – устройств, предназначенных для измерения времени. Действие любых часов основано на повторяющихся процессах – колебаниях. Чем меньше период (время одного полного колебания), тем часы более точные.
При изучении быстро протекающих процессов требуется измерять миллиардные и еще более мелкие доли секунды. Для этого служат атомные часы.
Ученик седьмого класса, конечно же, умеет измерять длину и время, массу продуктов определяют продавцы с помощью весов.
По мере изучения физики будет идти знакомство с различными физическими величинами, способами и приборами их измерения. А сейчас надо знать:
- чтобы измерить физическую величину, ее надо сравнить с однородной величиной, принятой за единицу;
- за основу физических величин берутся эталонные значения, то есть образец сравнения.
- для всех величин существуют свои способы, устройства и единицы измерения.
Числа «карлики» и числа «великаны»
Солнечная система. Лапка мухи под микроскопом.
Чтобы достать до Альфа Центавры, звезды, ближайшей к Солнечной системе, надо со скоростью света (300 000 км/с) лететь четыре года. Расстояния до небесных тел огромны.
Если определить расстояние от Земли до Солнца, то оно выразится числом 150 000 000 000 м. А бывают числа с еще большим количеством нулей. Масса Земли в килограммах выражается числом с 24 нулями. Такие числа называют «гигантами». Их записывать и использовать очень неудобно.
Существует способ краткой записи больших чисел в виде степени. Например, 1 000 000 = 10 6 . 10 – основание, а 6 – показатель степени.
Используя этот способ, расстояние от нашей планеты до Солнца запишется так:
150 000 000 000 = 15 ∙ 10 10 м – это промежуток называется астрономической единицей (1 а.е.) и служит единицей сравнения в Солнечной системе.
До Альфа-Центавры расстояние в 270 000 а.е., или 4 световых года. Световой год – это тоже астрономическая единица измерения расстояния. Астрономия – наука о космосе и космических телах. (1 св. год = 9,46 ∙ 10 15 м = 68 000а.е.).
Фото двойной звезды Альфа созвездия Центавра. (Источник)
Большие числа записываются при помощи кратных приставок. Например, километр – это тысяча метров, килограмм – тысяча граммов. Приставка «кило» обозначает «тысяча». Есть и другие приставки, которые обозначают умножение величины на число, кратное десяти. Примеры и форма записи даны в таблице кратных приставок.
Используя эти приставки можно записывать очень большие числа.
1 а.е. = 150 000 000 000 м = 150 ∙ 10 9 м = 150Гм;
1 св. год = 9 460 000 000 000 м = 9,46 ∙ 10 12 м = 9,46 Тм;
А теперь о числах – «карликах». Если сделать попытку измерить толщину одного листа книги, то сразу это не получится. Надо действовать по простому плану:
- отобрать в книге некоторое число страниц N (N = 100, например);
- измерить толщину L этих страниц (пусть L = 11 мм);
- найти толщину одной страницы d по формуле d = L/N.
Получится d = 0,11 мм = 0, 00011 м. Это число очень маленькое.
Такой способ измерения малых величин называется методом рядов. Он достаточно прост.
Размеры пшена. Толщина проволоки.
Но существуют и гораздо меньшие величины. Маленькие числа, так называемые «карлики», также записывают при помощи степеней или дольных приставок. (С приставками деци, санти, милли знакомятся еще в начальной школе).
Число меньше единицы, поэтому показатель степени – отрицательное число. Оно показывает количество цифр после запятой. Например, 0, 00011 м = 11 ∙ 10 -5 м.
Число 0,00000625 можно записать по-разному, применяя степень:
625 ∙ 10 -8 , 62,5 ∙ 10 -7 , 6,25 ∙ 10 -6 и т. д.
Очень маленькие числа по-другому можно записывать, используя таблицу дольных приставок.
Например, при изготовлении сверхточных приборов (телескопов, микроскопов и др.), детали ошлифовываются до очень гладкой поверхности. Неровности должны быть меньше 2,5 ∙ 10 -6 м или 2,5 мкм.
Большие и маленькие числа помогают человеку в различных отраслях деятельности: в науке, промышленности, медицине и т.д.
Как измерить длину. Погрешности измерений
На практике измерить длину отрезка достаточно просто:
- Приложить линейку к отрезку.
- Совместить ноль с началом отрезка.
- Определить число, соответствующее концу отрезка.
- Записать результат измерения.
В приведенном примере длина отрезка 9,9 см. Как точен этот результат? Он точен до 1 мм, так как на линейке нет меньших делений. Не надо путать значения слов «штрих» и «деление».
Численное значение самого маленького деления шкалы прибора называется ценой деления.
Чтобы определить цену деления прибора (например, линейки), нужно взять любые два рядом стоящие числа и их разность поделить на число делений между ними (т.е. промежутков между штрихами).
Цена деления линейки = (7 см – 6 см)/10 = 0,1 см = 1 мм.
И чтобы начать измерение, прежде всего надо найти цену деления прибора, который используется в данном случае. Любое измерение дает некоторую погрешность, зависящую от качества прибора. Поэтому ее называют погрешностью прибора.
Шкалы различных приборов. (Источник)
Известно, что измерить какую-то величину – это значит сравнить ее с эталоном. На практике пользуются не эталонами, а специальными приборами (линейка, часы и др.), которые являются копиями с эталонов, изготовленными с определенной точностью. Абсолютно точных измерений не бывает.
При использовании линейки допускается погрешность отсчета, которая равна половине цены деления прибора (0,5 мм). Сумма погрешностей прибора и отсчета называется абсолютной погрешностью. Она равна цене деления прибора.
Абсолютная погрешность обозначается значком Δ (дельта). Для школьной линейки Δ = 1 мм. Δ показывает, на сколько совершается ошибка при использовании того или иного прибора. Для более точных измерений используется штангенциркуль. В устройстве штангенциркуля заложено две шкалы, неподвижная (Δ = 1 мм) и подвижная (Δ = 0,1 мм).
А вот при помощи микрометра, где используется не перемещение шкалы, а ее вращение измерить длину можно с точностью до 0,01 мм. Но это еще не предел. В очень точных технологиях определяются размеры с точностью до 10 -7 м, в научных разработках точность возрастает во много раз. Но для этого нужны сверхточные приборы.
На практике, используя приборы, необходимо учитывать качество измерения. Величина, которая помогает это учесть, называется относительной погрешностью σ (сигма) и выражается в процентах.
σ = Δ / L ( L – измеренная величина)
Пример: Требуется замерить длину L отрезка различными приборами: 1) линейкой, 2) штангенциркулем и 3) микрометром. Длина отрезка получилась 55 мм. Какова относительная погрешность этих трех измерений?
1) Δ1 = 1 мм, L = 55 ± 1 мм, σ1 = 1 мм / 55 мм ≈ 0,018 (1,8%);
2) Δ2 = 0,1 мм, L = 55 ± 0,1 мм, σ2 = 0,1 мм / 55мм ≈ 0,0018 (0,18);
3) Δ3 = 0,01 мм, L = 55 ± 0,01 мм, σ3 = 0,01 мм / 55мм ≈ 0,00018 (0,018%).
Как видно, более точный прибор (микрометр) дает меньший процент ошибки.
Для каждого конкретного измерения в технике, практической деятельности человека и в науке существует своя точность измерения, в соответствии с которой применяются измерительные приборы.
Площадь и ее измерение
С измерением длин очень тесно связано измерение площадей. Из математики известны формулы площадей квадрата и прямоугольника. У квадрата все стороны равны, поэтому достаточно измерить одну сторону, а у прямоугольника противоположные стороны равны, поэтому надо знать длину и ширину. Площадь обозначается буквой S, и формулы для расчета площадей следующие:
Sкв = a 2 , Sпр = а ∙ в. Единицей измерения площади является квадратный метр (м 2 ).
Для измерения малых площадей применяются см 2 и мм 2 , а большие площади – в км 2 . В сельском хозяйстве для измерения земельных участков используют внесистемные единицы: гектар (га) – для больших, ар (а) или «сотка» — для небольших (приусадебных или дачных) участков земли. 1га = 10 000 м 2 , 1 а = 100 м 2 .
Очень часто на практике имеют дело с различными кругами. Это может быть цирковая арена, крышка стола, разрез ствола дерева. Формула нахождения площади круга: S = πR 2 . (π (пи) – это бесконечная дробь ≈ 3,14 подробно изучается в курсе алгебры).
Арена цирка. Круглый стол. Спил дерева.
А как определить площадь, ограниченную произвольной кривой линией? Такая площадь может быть у озера, полянки в лесу, листочка с дерева.
Существует правило нахождения площади тел произвольной формы:
- Разбить всю поверхность на равные квадраты с известной площадью.
- Подсчитать количество целых квадратов.
- Подсчитать число нецелых квадратов и поделить это число на два. (Это будет примерное количество целых квадратов).
- Сложить результаты пунктов 2 и 3.
- Умножить площадь одного квадрата на общее число целых квадратов.
Площадь больших территорий изображают в условном масштабе или фотографируют, применяют прием разбиения на квадраты и находят площадь фотографии. Используя масштаб вычисляют реальную площадь поверхности.
Довольно часто площадь приходится находить в географии. Каждое государство, область, город имеют свои площади. В строительстве – любое здание имеет площадь, которую необходимо знать строителям. В сельском хозяйстве ведется постоянный учет площадей для посевных культур.
Измерение объема. Мензурка
При измерении пространства нужно перейти к трем измерениям, так как представление о пространстве дает объем. Известны формулы объемов параллелепипеда, куба, шара, цилиндра.
Объем любого тела измеряется в кубических метрах (есть кратные и дольные единицы). Из математики известны формулы объемов:
Vпар = а ∙ в ∙ с (произведение длины, ширины и высоты),
Vк = а 3 (а — ребро куба),
Vцил = π ∙ r 2 ∙ h (r — радиус основания, h – высота цилиндра),
Vш = 4/3 π ∙ R 3 (R – радиус шара).
О вычислении объемов более сложной, но правильной, формы рассказывается в старших классах. А как определить объем, например, камня, форма которого может быть самой различной? Для измерения объемов таких тел используется специальный и очень простой прибор, который называется мензурка (или измерительный цилиндр). Это стеклянный сосуд с делениями.
При помощи этого цилиндра легко найти объемы сыпучих тел и жидкостей. Для этого достаточно их засыпать вещество или налить в мензурку жидкость и, зная цену деления, определить объем.
На мензурке обычно ставится единица измерения в миллилитрах. Литр – это широко применяемая единица объема, равная одной тысячной кубического метра. 1 мл = 1 см 3 = 10 -6 м 3 .
Определить объем камня или любого другого тела неправильной формы с помощью мензурки можно при условии, что тело имеет размеры, позволяющие опустить его в мензурку.
Налить в мензурку воду и зафиксировать ее объем. Прикрепить тело неправильной формы к нити. Осторожно опустить полностью в воду. Уровень воды поднимется ровно на столько, чему равен объем тела.
Пользуясь измерительным цилиндром, нельзя забывать, что это прибор, имеющий шкалу, а значит, результат получится с погрешностью.
Источник: 100urokov.ru
Объем

Объем , в науке физической или математической , является величиной , которая измеряет степень объекта или части пространства .
- В физике объем объекта измеряет «протяженность в физическом пространстве », которую он имеет во всех трех направлениях одновременно, точно так же, как площадь фигуры на плоскости измеряет «протяженность. в то же время.
- В математике объем части геометрического пространства является ее мерой в смысле теории меры Лебега .
Резюме
Измерение объема
- Физический объем измеряется в кубических метрах в Международной системе единиц . Литр часто используется , особенно для жидкостей и сухих материалов . Таким образом, объем рассматривается как экстенсивная величина, а связанной термодинамическиинтенсивной величиной является давление .
- В математике, а точнее в евклидовой геометрии , объем параллелепипеда, образованного тремя некопланарными векторами , вычисляется с использованием смешанного произведения трех векторов: ( v → 1 , v → 2 , v → 3 ) > _ , > _ , > _ )>
Вычисления объемов развивались на протяжении всей истории вслед за развитием математических вычислений . Так были рассчитаны первые объемы с использованием метода исчерпания , затем с использованием принципа Кавальери и, наконец, путем вычисления тройных интегралов .
Для простых тел ( параллелепипедов и объектов вращения) существуют математические формулы для определения их объема в соответствии с их характерными размерами.
Физический размер
Объем — это аддитивная величина: объем физической системы — это сумма объемов ее частей. С другой стороны, это не алгебраическая величина: физически не существует «отрицательного объема» (из которого была бы сделана дорожная сумка Мэри Поппинс ), суперпозиция которого с физической системой положительного объема дала бы систему, состоящую из объема в глобальном масштабе равен нулю или, по крайней мере, уменьшен: все тома имеют одинаковый знак и по соглашению считаются положительно. Именно по этой причине в формуле смешанного продукта результат берется в абсолютном значении.
Физическая интерпретация смешанного продукта заключается в том, что физический объем — это скалярное произведение поверхности на смещение :
Смещение является вектором , но ориентированная поверхность является псевдовектором , так что теоретически определенный таким образом объем является величиной, которая меняет знак, когда система подвергается косвенной изометрии (например, зеркальной симметрии). Фактически, если, например, объем сферы равен 4 ⁄ 3 π R 3 , полярная инверсия фактически изменит R на –R и логически приведет к отрицательному объему. В терминах размерного уравнения и с учетом величины ориентации смещение представляет собой вектор размерности L · 1 x, а площадь — псевдовектор размерности L 2 · 1 y , произведение двух представляет собой псевдоскаляр размерности L 3 · 1 z , т.е. имеет тот же характер, что и поток.
Физика остается практически неизменной, если все объемы подсчитываются отрицательно, но на практике физические объемы считаются положительно, что равносильно умножению объема в предыдущем смысле на символ Леви-Чивита (сам в 1 z ). Тогда объем физического тела является истинным скаляром из-за соглашения об ориентации. Аналогичным образом, хотя элемент поверхности обычно является псевдовектором в 1 y , соглашение об ориентации, которое требует, чтобы его ориентация на замкнутой поверхности была направлена наружу, сводится к умножению его на соглашение об ориентации в 1 z , что затем делает его вектор истинным в 1 х . Использование этого соглашения об ориентации может быть проблематичным в анализе размеров , поскольку оно соответствует количеству, которое в противном случае обычно невидимо в данных задачи.
Элементарный объем
Область размерности 3 обычно описывается тремя независимыми параметрами u , v и w . Для любой точки M ( u , v , w ), принадлежащей этой области, вектор положения (где O обозначает любое фиксированное начало координат) имеет для дифференциала : О M → >>>
Элементарное изменение d u , d v , d w ) трех параметров образует элемент объема (или элементарного объема ) d 3 V (или просто d V, если нам не нужно помнить, что три переменные изменяются независимо), определяемый формулой :
Декартовы координаты
В ортонормированных декартовых координатах текущая точка M идентифицируется по x , y и z , так что:
где , и — фиксированные единичные векторы трех ортогональных осей (и, взятые в этом порядке, образуют прямой трехгранник). Тогда у нас есть: Икс ^ >> y ^ >> z ^ >>
Мы легко можем сделать вывод, что:
Цилиндрические координаты
В цилиндрических координатах текущая точка M обозначается буквами r , φ и z , так что:
где — единичный вектор оси O z ортонормированной системы координат, а единичный вектор имеет декартовы координаты cos ( φ ) , sin ( φ ) и 0 . Тогда у нас есть: z ^ >> р ^ ( φ ) > ( varphi)>
где — единичный вектор декартовых координат –sin ( φ ) , cos ( φ ) и 0 . Векторы , и являются унитарными и ортогональны в паре (и, взятом в таком порядке, образуют прямую трехгранника). Мы легко можем сделать вывод, что: φ ^ ( φ ) > ( varphi)> р ^ ( φ ) > ( varphi)> φ ^ ( φ ) > ( varphi)> z ^ >>
Сферические координаты
В сферических координатах текущая точка M обозначается символами ρ , θ и φ , так что:
где единичный вектор имеет декартовы координаты sin ( θ ) cos ( φ ) , sin ( θ ) sin ( φ ) и cos ( θ ) . Тогда у нас есть: ρ ^ ( θ , φ ) > ( theta, varphi)>
где — единичный вектор декартовых координат cos ( θ ) cos ( φ ) , cos ( θ ) sin ( φ ) и –sin ( θ ) , а вектор координат –sin ( φ ) , cos ( φ ) и 0 . Векторы , и унитарны и попарно ортогональны (и, взятые в таком порядке, образуют прямой трехгранник). Мы легко можем сделать вывод, что: θ ^ ( θ , φ ) > ( theta, varphi)> φ ^ ( φ ) > ( varphi)> ρ ^ ( θ , φ ) > ( theta, varphi)> θ ^ ( θ , φ ) > ( theta, varphi)> φ ^ ( φ ) > ( varphi)>
Единицы объема
Единицей объема в Международной системе является кубический метр (м 3 ) и его производные (дм 3 , см 3 , мм 3 ). Но другие единицы объема сохраняются, особенно в англосаксонских странах (см. Преобразование единиц ).
Объемы жидкого материала часто имеют собственные единицы ( литр , пинта , бочка ). Внедрение метрической системы значительно упростило количество используемых единиц объема, которых в Ancien Régime было более двадцати (см. Единицы измерения Ancien Régime ).
Для газов, где мы хотим знать количество вещества (количество молекул), содержащегося в данном объеме, независимо от давления и температуры, существуют два определения поправки :
- так называемый нормальный кубический метр, выраженный в м 3 (н), соответствующий объему газа, находящемуся под давлением 1013,25 гПа (давление нормальной атмосферы или 1 атм ) и температуре 0 ° C ;
- сказал стандартный кубический метр выражается в м 3 (с) , что соответствует объему газа под пониженным давлением 1 013.25 гПа (нормальное атмосферное давление или 1 атм ) и температуру 15 ° C .
Описанные выше тома соответствуют так называемым скорректированным томам. Объем, не учитывающий эти поправки, называется валовым. Эти объемы находятся в зависимости от расхода и теплотворной способности газов.
В Европейском Союзе многие объемы (и массы) потребительских товаров указаны в приблизительных количествах . Они отмечены как таковые строчной буквой «е» .
В математике единица объема не фигурирует в формулах. Он неявно задается объемом единичного куба . Если, например, из соображений масштаба единичный куб имеет край 2 см , объем X единичных кубов соответствует 8 X см 3 .
Некоторые формулы
- V объем фигуры;
- по краю;
- B и b — площади большого основания и малого основания;
- H высота (или расстояние, разделяющее две грани);
- D или d диаметр;
- R или r радиус;
- L или l длина и ширина прямоугольника.
В Платоновых тела
Это единственные пять правильных выпуклых многогранников. Их соответствующие объемы задаются следующими формулами:
Призмы и цилиндры
Общая формула всегда такова: V = B × H (объем = площадь основания × высота), независимо от того, прямая призма или цилиндр или нет.
- для параллелепипеда или клавиатуры: , V знак равно L × ℓ × ЧАС
- для кругового цилиндра : V = π R 2 × Н .
В пирамиды и конусы
Общая формула всегда: V = 1 / 3 В × Н .
- Конус вращения : V = π / 3 R 2 × H .
- Пирамиды усечены плоскость , параллельная основанию: . V знак равно ЧАС 3 ( B + б + B б ) > left (B + b + > right)>
- Объем шараV = 4 / 3 π R 3 или V = π D 3 / 6 .
- Для сферической крышки, или где R — радиус шара, r — радиус крышки, а H — высота крышки. V знак равно π 3 ЧАС 2 ( 3 р — ЧАС ) > H ^ (3R-H)> V знак равно π 2 ЧАС ( ЧАС 2 3 + р 2 ) > H left (< frac > + r ^ right)>
- Объем цилиндра , образованного с шаром (салфетку кольцо) не зависит от радиуса шара , но только высота Н цилиндра: . V знак равно π 6 ЧАС 3 > H ^ >
- Сферический сектор (пересечение конуса с вершиной O и шара с центром O: где H — высота колпачка, а R — радиус шара. V знак равно 2 3 π р 2 ЧАС < displaystyle V = < frac > pi R ^ H>
Тела революции
Теорема Гулдина (или правила Паппа) дает возможность вычислить объем тела вращения порожденного вращения на элементе поверхности S плоскости вокруг оси , расположенной в плоскости , а не пересекая его, мало что известно центр тяжести G на поверхность элемента S .
Эта формула позволяет определить следующие объемы:
- тор : где R представляет собой радиус окружности с центром О , вращающимися вокруг оси (А) , и где R представляет собой расстояние от G до (А) . V знак равно 2 π 2 р р 2 Rr ^ >
- ствол: Кеплер дает приблизительную формулу для объема ствола , которая оказывается точной, когда ствол создается сферой, пирамидой, однополостным гиперболоидом , эллиптическим параболоидом , эллипсоидом вращения. Если B1 и B2 — это поверхности оснований, а B3 — поверхность сечения на средней высоте, то
Другой
- Правый круговой коноид (пример резцы): где R представляет собой радиус основной окружности и H высоту коноида. V знак равно 1 2 π р 2 ЧАС > pi R ^ H>
- Слитка ( шестигранники , образованный двумя параллельными прямоугольными основаниями и 4 трапецеидальных боковых граней). Мы находим формулу Кеплера: где B1 и B2 — площади двух прямоугольных оснований, а B3 — площадь сечения на средней высоте. Эта формула широко используется в гражданском строительстве при расчетах объема земляных работ и, в частности, при перемещении земли в области общественных работ . V знак равно час 6 ( B 1 + B 2 + 4 B 3 ) > (B_ + B_ + 4B_ )>
Объемный и интегральный расчет
Если — ограниченная часть , объем цилиндра, имеющего в качестве образующей границу , ограниченную плоскостью z = 0 и поверхностью уравнения z = ‘f ( x , y ) — с положительным и непрерывным f, — равен: D >> р 2 ^ > D >> D >>
В случае, когда область определяется простыми условиями x 1 < x < x 2 , y 1 ( x ) < y ( x ) < y 2 ( x ) , этот расчет сводится к следующему: D >>
В случае, когда область определяется простыми условиями x 1 ( z , y ) < x ( z , y ) < x 2 ( z , y ) , y 1 ( z ) < y ( z ) < y 2 ( z ) и z 1 < z < z 2 , этот расчет сводится к следующему: В >
По линейности интегрирования трудно определить область, которая может быть разделена на несколько подобластей, которые могут быть выражены в простых условиях.
Если область лучше всего выражается в цилиндрических координатах с помощью простых условий , расчет можно выразить следующим образом: В > В ′ ‘>
Если область лучше всего выражается в сферических координатах с помощью простых условий , расчет можно выразить следующим образом: В > В ″ »>
В случае, когда область представляет собой твердое тело вращения, граница которого образована вращением кривой уравнения y = ‘f ( x ) вокруг оси ( Ox ), вычисление объема сводится к простому интегралу: В >
Источник: ru.frwiki.wiki