Как используются пределы в строительстве

Курс «Где используется предел…» предназначен для учащихся 10-11-х классов общеобразовательных учреждений, проявляющих интерес к математике, желающих повысить свой математический уровень, расширить и углубить предметные знания. Концепция данной программы заключается в пропедевтике темы «Пределы», изучаемой в большинстве вузов (как технической, так и гуманитарной направленности). Как показывает опыт, большая часть студентов испытывает трудности при изучении данной темы, так как школьная программа охватывает ее только поверхностно, основываясь на интуиции и наглядных представлениях. Отличительной особенностью данного элективного курса от уже существующих является наличие в нем задач прикладного характера.

• создание мотивационной основы для осознанного выбора дальнейшего профиля обучения,
• формирование образовательных, коммуникативных и информационных компетентностей для продолжения математического образования в вузах различного профиля.

Реализация поставленных целей будет способствовать овладению учащимися основами математической культуры, становлению личности.

✓ Предел функции. Определение предела функции «по Коши» и «по Гейне» | матан #014 | Борис Трушин

• изучить способы вычисления пределов;
• отработать навыки применения данных знаний при решении задач различной сложности;
• отработать навыки самостоятельной работы, работы в малых группах;
• отработать навыки работы со справочной литературой, с компьютером;
• отработать умения и навыки исследовательской работы;
• способствовать развитию алгоритмического мышления учащихся;
• организовать встречу со студентами, изучающих математику в вузе .

Сроки реализации – 36 часов (1 час в неделю).

Содержание курса включает в себя теоретическую и практическую части.

В основу теоретической части положены темы, включенные в профильный курс математики в разделе “Начала математического анализа” и дополненные темами, расширяющими и углубляющими предмет: Бесконечно малые и бесконечно большие величины, Конечный предел, Бесконечный предел, Понятие бесконечности, Элементарные приемы раскрытия неопределенностей, Второй замечательный предел, Прикладные задачи с использованием второго замечательного предела, Сравнение бесконечно малых, Точки разрыва функции, Правило Лопиталя (перечислить!)

Для реализации данного содержания используются методы активного обучения (проблемный, исследовательский, частично-поисковый), развивающие познавательную самостоятельность, интеллектуальную активность и творческую направленность.

Для развития образовательных и информационных компетентностей у учащихся ведущими являются такие формы организации учебной деятельности как лекция, практикум, семинар, круглый стол. Преобладающими приемами организации учебной деятельности будут: создание проблемной ситуации, имеющей форму познавательной задачи; общение диалогического типа, предметом которого является вводимый учителем материал.

Практическая часть курса предполагает использование поисковой и элементов исследовательской деятельности при работе с различными источниками информации (учебными пособиями, справочники, энциклопедии, Интернет-ресурсами), отборе и переработке информации для написания реферативных работ по избранным вопросам математики. Для создания условий успешности учитываются реальные учебные возможности учащихся через дифференцированные варианты заданий для проверочной, самостоятельной работы и для подготовки к семинарам.

Заставили снести кирпичный гараж на два автомобиля

Курс направлен на достижение метапредметных результатов, – в частности, на формирование надпредметных и обобщенных способов совместной деятельности, умение работать в группе, умение выстраивать свой ответ, доказывать и аргументировать свою точку зрения, участвовать в дискуссии и оппонировать. На занятиях предполагается разумное сочетание различных форм обучения:коллективной, групповой, парной и индивидуальной.

В результате изучения курса “Где используется предел…” учащиеся должны

– определение последовательности, предела последовательности, бесконечно малой и бесконечно большой величины;
– определение предела функции, свойства пределов функции;
– прикладное значение теории пределов.

– вычислять несложные пределы последовательностей и функций в точке и на бесконечность;
– находить простейшие пределы с использованием первого и второго замечательных пределов и правила Лопиталя; использовать элементарные приемы для раскрытия неопределенностей;
– исследовать функции – на непрерывность;
– решать прикладные задачи с помощью теории пределов.
– осуществлять поиск математической информации по определённой теме в различных источниках;
– подготовить доклад;

В процессе обучения используются средства: учебные пособия: Запорожец Г. И. «Руководство к решению задач по математическому анализу», средства наглядности, компьютерные технологии.

• текущий контроль (беседы по изученным темам, тестирование, диктант по теоретическому материалу);
• зачётный практикум (индивидуальные домашние задания, дифференцированные
• самостоятельные работы, проверочные работы, проект);
• итоговый (выполнение контрольной работы).

Учебно-тематический план

Содержание курса:

1. Вводное занятие.

2. Числовая последовательность. Предел последовательности.(2 часа)

Определение числовой последовательности. Формула общего члена последовательности. Определение числовой последовательности. Свойства пределов числовой последовательности: предел суммы, произведения, частного последовательностей. Примеры на вычисление пределов числовой последовательности.

3. Бесконечно малые и бесконечно большие величины.(2 часа)

Определение бесконечно малых и бесконечно больших величин. Нахождение пределов с использованием бесконечно малых и бесконечно больших величин.

4. Конечный предел. Бесконечный предел. Понятие бесконечности. (2 часа)

Понятие конечного предела. Понятие бесконечного предела.

5. Предел функции.(2 часа)

Определение предела функции в точке. Вычисление предела функции в точке. Предел функции на бесконечность.

6. Теоремы о бесконечно малых и о пределах. (2 часа)

Теоремы о бесконечно малых. Свойства пределов функции. Использование свойств при вычислении пределов функции.

7. Частные случаи нахождения пределов. (2 часа)

Простейшие пределы, как формулы для вычисления пределов и их применение.

8. Элементарные приемы раскрытия неопределенностей.(3 часа)

Типы неопределенностей:.Прием сокращения дроби на множитель, стремящийся к нулю. Теорема Безу. Прием вынесения за скобки множителя с наивысшей степенью. Использование приемов для раскрытия неопределенностей.

9. Первый замечательный предел. (2 часа)

Первый замечательный предел. Использование первого замечательного предела при вычислении пределов.

10. Второй замечательный предел. (2 часа)

Второй замечательный предел. Использование второго замечательного предела при вычислении пределов.

11. Практические задачи с использованием второго замечательного предела (4 часа)

Понятие дискретного процента. Формула сложных процентов. Задачи на темы: рост вклада, рост населения страны, распад радиоактивного вещества, размножение бактерий.

12. Смешанные задачи на нахождение пределов. (2 часа)

Решение смешанных задач на вычисление пределов.

13. Сравнение бесконечно малых. (3 часа)

Как сравнить между собой бесконечно малые величины. Эквивалентность бесконечно малых. и их свойства. Нахождение пределов с помощью свойств.

14. Непрерывность и точки разрыва функции. (3 часа)

Определение непрерывной функции. Условие необходимости и достаточности непрерывности функции. Определение разрывной функции. Точки разрыва первого и второго рода. Исследование функции на непрерывность с помощью пределов.

15. Правило Лопиталя. (2 часа)

Правило Лопиталя. Нахождение пределов с помощью правила Лопиталя. Сравнительный анализ способов раскрытия неопределенностей одного вида.

Источник: urok.1sept.ru

Как используются пределы в строительстве

2. Кремер Н.Ш., Путко Б.А., Тришин И.М. Математика для экономистов: от арифметики до эконометрики. – М., 2007. – 145-187 с.

3. Музенитов Ш.А., Синельников М.Б., Музенитов Э.Ш. Математическая экономика. – Ставрополь, 2003. – 11-75 с.

4. Гулай Т.А., Долгополова А.Ф., Литвин Д.Б. Совершенствование математической подготовки студентов аграрных вузов // Инновационные векторы современного образования, 2012. – С. 11-16.

5. Гулай Т.А., Долгополова А.Ф., Литвин Д.Б., Донец З.Г. Экономико-математическое моделирование факторов экономического анализа посредством метода линейного программирования // Аграрная наука, творчество, рост: Сборник научных трудов по материалам IV Международной научно-практической конференции / Отв. за вып. Башкатова Т.А., 2014. – С. 329-332.

6. Гулай Т.А., Долгополова А.Ф., Литвин Д.Б. Анализ и оценка приоритетности разделов математических дисциплин, изучаемых студентами экономических специальностей аграрных вузов // Вестник АПК Ставрополья. 2013. – № 1 (9). – С. 6–10.

Понятие предела несомненно занимает ключевое место в математике. Оно является основным понятием математического анализа, без которого невозможны многие экономические расчеты. Представление о понятии предела является очень древним, основанным на эмпирических исследованиях, а современная теория – результат систематизации и эволюции этих представлений. Такие математики древности, как Евклид и Аристотель, выдвигали идею существования предела. Но лишь спустя несколько столетий Ньютон обратил внимание на эту идею и ввел термин limes (предел).

Определение предела последовательности

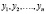
Число a называется пределом последовательности , если по мере возрастания номера n член yn неограниченно приближается к a:

.

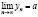
Теория пределов часто используется в различных экономических вычислениях, например, в подсчитывании сложных процентов.

В основном практических расчетах применяют дискретные проценты (начисляемые с определённой периодичностью). Время – дискретная переменная. В некоторых случаях возникает необходимость в применении непрерывных процентов (например, в доказательствах расчётов, в которых происходят непрерывные процессы). Рассмотрим формулу сложных процентов

,

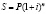
где P – первоначальная сумма; i – ставка процентов (десятичная дробь); S – сумма, которая образовалась к концу срока ссуды в конце n-го года.

Пример. Найти прибыль от 30000 долларов, положенных на депозит на 3 года под 10 % годовых, если в конце каждого года проценты добавлялись к депозитному вкладу.

Решение. Используем формулу для вычисления сложных процентов:

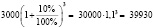
долл.

В данном случае прибыль будет равна:

39930 – 30000 = 9930 долл.

Ответ: 9930 долл.

Зачастую в финансовой практике возникают задачи, обратные определению наращенной суммы: по заданной сумме, которую следует уплатить через некоторое время, необходимо определить сумму полученной ссуды. Имеем:

,

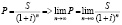
где S – заданная сумма; n – время; P – полученная ссуда.

Следовательно, при очень больших сроках платежа сумма последнего будет крайне незначительна. В финансово-кредитных операциях непрерывные процессы наращения денежных сумм почти не используются, однако при выборе и обосновании инвестиционных решений они необходимы (многие экономические явления по своей природе непрерывны). Разновидность формулы сложных процентов в случае, когда проценты начисляются m раз в году:

,

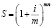
где m – число периодов начисления в году, i – годовая ставка.

Логично, что чем больше m, тем меньше n между моментами начисления процентов. В пределе при m →∞ имеем:

.

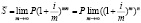
Так как , то .

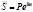
Чтобы было возможно отличать ставки непрерывных и дискретных процентов, непрерывную ставку обозначим d, тогда .

Пределы так же применяются при использовании производной в экономике. Если функция u=u(t) – объем произведенной продукции за время t, то производная u›(t0) есть производительность труда в момент времени t0. Если y=f(x) – издержки производства при производстве xединиц продукции, то производная y›=f›(x0) выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство дополнительной продукции. Также существуют другие величины, характеризующие предельные процессы выручки, дохода, продукта, полезности, производительность и т.д.

Если предельные издержки и цена продукции равны, то в таких случаях говорят, что выпуск продукции является оптимальным для производителя.

,

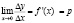
где ?y – изменение денежных единиц, ?x – изменение выпуска продукции, p – цена продукции.

Рассмотрим соотношение между предельным и средним доходами. Пусть p – цена, а q–количество продукции, тогда r = pq, где r – суммарный доход.

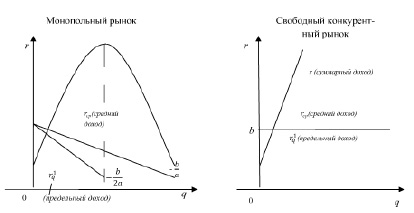
Рассмотрим монопольный рынок (на цену влияет одна фирма (иногда несколько): пусть p=aq+b – кривая спроса, тогда r=(aq+b) q=aq2+bq – суммарный доход, – средний доход, – предельный доход. В таких условиях действует следующая закономерность: чем большее количество продукции продано, тем предельный доход ниже, а значит и средний доход уменьшается.

В условиях свободного конкурентного рынка товары продают по фиксированной цене (p=b), тогда r = bq – суммарный доход, – предельный доход, – средний доход. Значит, при совершенной конкуренции предельный и средний доходы совпадают.

От 0 до эластичный спрос, от до – неэластичный спрос.

Эластичностью функции Ex(y) называется предел отношения относительного приращения функции y к относительному приращению переменной x при ?x→0:

.

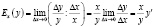
Эластичность функции приближенно показывает, на сколько процентов изменится функция y = f(x) при изменении переменной x на 1 % (другими словами, эластичность показывает, на сколько процентов в среднем произойдет изменение спроса при изменении цены на 1 %). Если модуль найденной эластичности больше единицы, то спрос эластичный (); если меньше либо равен единице, тогда спрос называют неэластичным (); если равен единице, то говорят о спросе с единичной эластичностью .

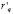
При p = p(q) – произвольной кривой спроса, предельный доход () равен:

= ,

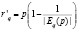
так как Ep(q) < 0.

C возрастанием цены р суммарный доход от продажи продукции увеличивается (при эластичном спросе (, то )) или уменьшается (при неэластичном спросе (, то )).

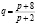
Пример: даны функции спроса и предложения s = p + 0,5, где p – цена товара, q – количество покупаемого товара (спрос), а s – количество предлагаемого товара (предложение). Найти рыночную цену и эластичность спроса и предложения для этой цены.

Решение. Рыночную цену найдем с помощью равенства q иs:

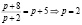
(ден. ед.).

Эластичность спроса и предложения найдем по формуле

–

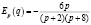
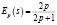
эластичность спроса, – эластичность предложения.

Т.к. p = 2, то , а . Значит, спрос и предложение на этот товар при рыночной цене являются неэластичными: при увеличении цены на 1 % спрос уменьшится на 0,3 %, а предложение возрастет на 0,8 %.

В ходе работы показана актуальность теории пределов при нахождении показателей в различных экономических ситуациях. Следовательно, теория пределов играет важную роль не только в математике, но и в экономике.

Источник: eduherald.ru

Что означает предел в математике

Кто о чём, а мы продолжаем разбирать сложную математику, чтобы она не была такой сложной.

Что такое предел в математике

Когда математики говорят о пределах, то имеют в виду такую последовательность событий:

1. Есть функция — это просто какая-то «коробка» с математикой. Ты ей на вход число, она его обрабатывает у себя внутри и отдаёт другое число.
2. У функции есть как минимум два числа: то, которое ты ей даёшь на вход; и то, которое получаешь на выходе.
3. Иногда математикам интересно, что будет, если число на входе будет к чему-то стремиться. А именно: «Если число на входе будет стремиться вот сюда, куда будет стремиться число на выходе?»

Самое простое объяснение функции в математике.

Стремиться — значит стараться приблизиться к какому-то числу, но не достигнуть его.

Если мы говорим, что переменная функции стремится к бесконечности, то это значит, что с каждым новым вычислением мы берём значение переменной больше предыдущего.

1, 2, 3, … 1000000000000003, 1000000000000004 и так до бесконечности

Наоборот тоже работает: если переменная функции стремится к нулю, то это значит, что она постоянно уменьшается:

1, 0.1, 0.01, 0.001, … 0.00000000000000000000000001 и с каждым разом число будет ближе к нулю, но никогда его не достигнет.

Стремление переменной к числу обозначается стрелкой: x→0, а предел — словом lim:

График и предел

Если мы нарисуем график этой функции, то можем увидеть, что начиная с какого-то момента он превратится в почти прямую линию вдоль оси. Почти прямую — потому что прямой он никогда не станет, но стремится к этому, если продолжить рисовать график бесконечно.

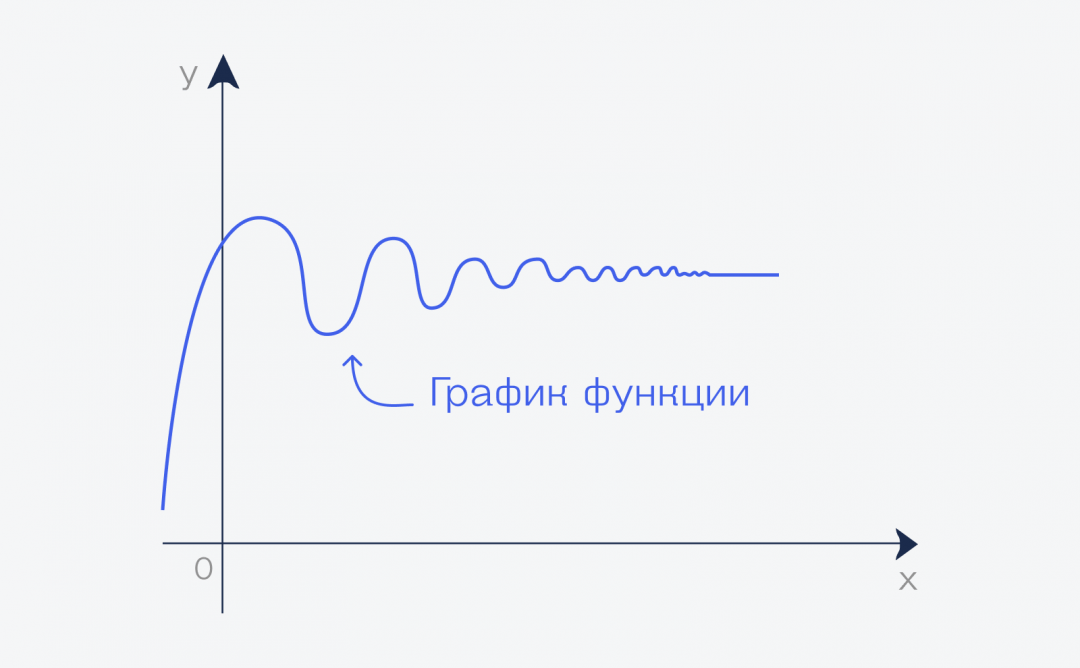
Но бесконечный график означает, что у нас переменная функции стремится к бесконечности. А значение этой линии на графике — это и есть предел этой функции при переменной, стремящейся к бесконечности:

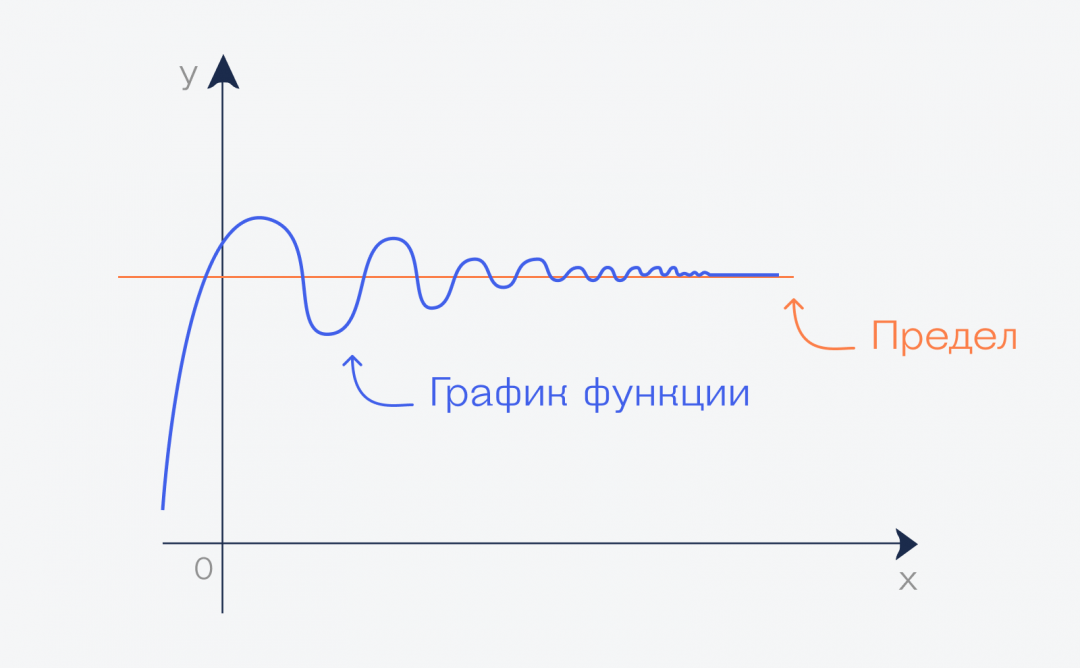
Пределы в жизни

Пределы из математики часто используются для решения практических задач, где нужно найти точку, после которой разница в результате будет уже незаметна.

Например, бригада монтажников строит мост, и им нужно понять, какой максимальной длины можно сделать плиту перекрытия. Есть требования, что плита должна выдерживать в середине нагрузку в 50 тонн — она может быть и прочнее, но 50 тонн это минимум. Для решения этой задачи используют предел — он покажет, длиннее какого размера делать плиту нельзя, а всё, что короче, даст необходимую прочность.

Астрономы с помощью пределов изучают законы Вселенной, физики проверяют всё на прочность, и даже в микроэлектронике затухание сигналов тоже зависит от пределов функций.

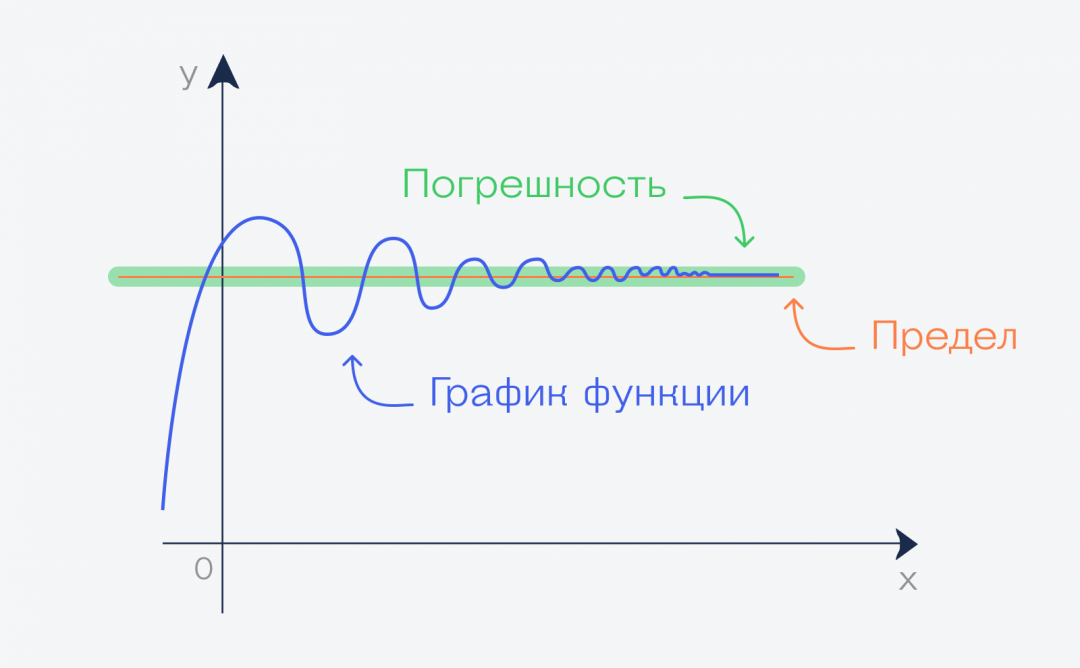
Погрешность в пределах

В математике пределы считаются точно: используются специальные формулы и трюки, которые помогают найти точный ответ. Но в жизни такая точность необязательна: можно взять любое решение, которое нас устроит с приемлемой погрешностью.

Эта погрешность поможет нам считать пределы, не зная точных математических формул подсчёта.

Считаем предел в программировании

Раз у нас есть постоянное действие по уменьшению или увеличению переменной, то логично сделать из этого простой цикл и поручить его машине. Единственное, что нам нужно предусмотреть, — момент, когда цикл должен остановиться, потому что в мире математики lim по умолчанию касается бесконечности (потому что стремиться можно бесконечно).

Так как мы не знаем заранее точного предела функции, но можем контролировать количество повторений, то сделаем такие условия для остановки цикла:

1. Закончилось количество повторений. Например, мы заранее говорим, что будем стремиться к границе предела 10000000000 раз, но если ничего не выйдет — остановимся.
2. Если достигли нужной погрешности. Два соседних результата отличаются на величину погрешности или меньше — отлично, мы нашли то, что нужно.

Самый сложный момент в коде — описать то, как переменная функции к чему-то стремится. Если к бесконечности, то всё просто: на каждом шаге прибавляем или умножаем на какое-то число. А если нужно, чтобы переменная стремилась к нулю или другому числу, то можно действовать так: брать начальное число, конечное, складывать их и делить пополам. Так мы будем постоянно приближаться к нужному нам числу, но никогда его не достигнем.

⚠️ Важная оговорка: числа в компьютере — это не числа в абстрактном математическом понимании, а конечный набор данных. Конечный он тем, что на всякое число выделяется какое-то количество «клеток», в которые это число можно записать. Если у нас ограниченное количество «клеток», значит, у нас есть какой-то предел самого большого и самого малого числа.

Например, если мы дали переменной 32 бита памяти, самое малое число, которое мы сможем в нее записать, — 1,4012985 × 10 -45 . Это кажется бесконечно малым, но на самом деле, если циклически делить число на 2 несколько сотен раз в секунду, мы упремся в этот лимит точности почти сразу. Потом знаки после запятой закончатся и число очень быстро превратится в 0.

С точки зрения математики любое число можно бесконечно делить и получать бесконечное число знаков после запятой; а с точки зрения компьютера бесконечное число знаков невозможно, и если делить достаточно долго — мы получим ноль.

Поэтому в работе с пределами важно указывать либо число шагов для определения предела, либо погрешность.

Теперь напишем простой цикл, который нам посчитает lim x→2 (8−2x) / (x²−4x−12):

• предел функции f(x) = (8−2x) / (x²−4x-12);
• при x стремящемся к 2.

Если мы посчитаем этот предел как математики, то получим значение −1. Проверим, как с этим справится наш код:

Источник: thecode.media

Пределы в математике для чайников: объяснение, теория, примеры решений

Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Понятие предела в математике

Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Lim — от английского limit — предел.

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Приведем конкретный пример. Задача — найти предел.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях?

Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Пусть есть предел:

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

• Контрольная работа от 1 дня / от 120 р. Узнать стоимость
• Дипломная работа от 7 дней / от 9540 р. Узнать стоимость
• Курсовая работа 5 дней / от 2160 р. Узнать стоимость
• Реферат от 1 дня / от 840 р. Узнать стоимость

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник: zaochnik.ru